Bonjour,
Pouvez vous me donner des pustes pour résoudre cet exercice svp car je ne vois pas du tt comment il faut faire, merci d avance.
On définit Z= (z-5i)/(z+3).
Determiner l ensemble des points M d affixe z tels que :
- Z soit un reel
- Z soit imaginaire pur
- Z ait un module egal a 1
- Z ait un argument egal a pi/2
Arguments/Modules
11 messages
- Page 1 sur 1
Re: Arguments/Modules
Mama27 a écrit: Z soit un reel
on peut commencer par écrire
Mama27 a écrit: Z soit imaginaire pur
on peut écrire
Mama27 a écrit: |Z| =1
|z-5i|=|z-(-3)|
Mama27 a écrit: Z ait un argument egal a pi/2
poser les points A d'affixe 5i et B d'affixe (-3)
Re: Arguments/Modules
D accord merci je vais essayer faire ca.
Mais comment savez vous qu il faut calculer cela ?
Mais comment savez vous qu il faut calculer cela ?
Re: Arguments/Modules
par exemple pour la question (1), on utilise le fait que les réels sont les nombres complexes égaux à leur conjugué.
puis après , si z=x+iy,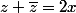 et
et 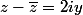
puis après , si z=x+iy,
Re: Arguments/Modules
Bonjour Mama27,
Pour savoir à quelle condition Z est un nombre réel on peut dans un premier temps le mettre sous forme algébrique puis trouver z (donc x et y) de sorte à annuler sa partie imaginaire.
Je t'ai fait une vidéo complète pour te montrer comment obtenir Z nombre réel !! Enjoy !
https://www.youtube.com/watch?v=0IbUFAD ... dex=7&t=0s
Dis-moi ce que tu en penses
Pour savoir à quelle condition Z est un nombre réel on peut dans un premier temps le mettre sous forme algébrique puis trouver z (donc x et y) de sorte à annuler sa partie imaginaire.
Je t'ai fait une vidéo complète pour te montrer comment obtenir Z nombre réel !! Enjoy !
https://www.youtube.com/watch?v=0IbUFAD ... dex=7&t=0s
Dis-moi ce que tu en penses
Re: Arguments/Modules
Bonjour;
Une autre façon de faire (mais qui utilise l'indication de Mathelot!) .
Tout d'abord , est définie si :
est définie si :  , donc si
, donc si \ne (-3 ; 0)) .
.
}{(x+3)+iy}=\dfrac{(x+i(y-5))((x+3)-iy)}{((x+3)+iy)((x+3)-iy)})
)((x+3)-iy)}{(x+3)^2+y^2}=\dfrac{x(x+3)+y(y-5)+i((x+3)(y-5)-xy)}{(x+3)^2+y^2}) .
.
 est un nombre réel si :
est un nombre réel si : (y-5)-xy=0\Rightarrow xy-5x+3y-15-xy=0)
 avec
avec  ;
;
donc :) avec
avec  ;
;
donc l'ensemble des points d'affixe
d'affixe  est :
est : ; x\in]-\infty;-3[\cup]-3;+\infty[\}) .
.
Tu peux répondre maintenant à la deuxième question .
Une autre façon de faire (mais qui utilise l'indication de Mathelot!) .
Tout d'abord ,
donc :
donc l'ensemble des points
Tu peux répondre maintenant à la deuxième question .
Re: Arguments/Modules
Hello Mama27,
Je t'ai même fait une vidéo pour voir comment obtenir Z imaginaire pur ! En effet il s'agit ici d’annuler la partie réelle mais c'est un peu délicat à cause du x^2 et y^2...
Bon visionnage et dis-moi si ça t'a bien aidé
https://www.youtube.com/watch?v=icwEN7M ... LZ1HZLwplO
Je t'ai même fait une vidéo pour voir comment obtenir Z imaginaire pur ! En effet il s'agit ici d’annuler la partie réelle mais c'est un peu délicat à cause du x^2 et y^2...
Bon visionnage et dis-moi si ça t'a bien aidé
https://www.youtube.com/watch?v=icwEN7M ... LZ1HZLwplO
Re: Arguments/Modules
pour le reel j ai compris mais pas la fin quand on trouve dans les coordonnées x, d'où vient il ?
alors que pour l imaginaire pur j avoue que je suis complétement perdue avait vous une autre facon de m'expliquer svp
mon prof nous a dit qu il y avait 2 facon de resoudre ces problemes, la premiere facon grace aux complexes et la deuxieme grace a la "geometrie" (je crois que c'etait ca mais je ne suis pas tout a fait sure)
alors que pour l imaginaire pur j avoue que je suis complétement perdue avait vous une autre facon de m'expliquer svp
mon prof nous a dit qu il y avait 2 facon de resoudre ces problemes, la premiere facon grace aux complexes et la deuxieme grace a la "geometrie" (je crois que c'etait ca mais je ne suis pas tout a fait sure)
Re: Arguments/Modules
Bonjour Mama27, en effet dans cet exemple il existe une autre méthode faisant intervenir la formule arg(zd-zc)/(zb-za) = angle orienté (AB, CD). Mais ceci ne marche que si on a un coeff 1 devant z.
Tout de même je te donnerai une solution détaillée avec la deuxième méthode d'ici demain matin.
Tout de même je te donnerai une solution détaillée avec la deuxième méthode d'ici demain matin.
Re: Arguments/Modules
Mama27,
Chose promise chose due, je t'ai fait une vidéo qui te montre comment obtenir Z réel sans passer par la forme algébrique ni de z ni de Z !!
A la place, on utilise la formule des angles orientés :
https://www.youtube.com/watch?v=GMm-ors ... LZ1HZLwplO
Enjoy et dis-moi si tu as bien compris
Chose promise chose due, je t'ai fait une vidéo qui te montre comment obtenir Z réel sans passer par la forme algébrique ni de z ni de Z !!
A la place, on utilise la formule des angles orientés :
https://www.youtube.com/watch?v=GMm-ors ... LZ1HZLwplO
Enjoy et dis-moi si tu as bien compris
Re: Arguments/Modules
Soyons fous, je te montre aussi comment faire pour obtenir Z imaginaire pur avec la formule des angles orientés !
https://www.youtube.com/watch?v=miZq7HC ... LZ1HZLwplO
https://www.youtube.com/watch?v=miZq7HC ... LZ1HZLwplO
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 76 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
