soit f: I vers R et d appartient à I
montrer que si f est dérivable en d alors pour toutes suites (an) et (bn) vérifiant:
(qqsoit n), an different de bn, an<d<bn et lim an=lim bn=d
alors,
lim (f(an)-f(bn))/(an-bn) = f'(d)
j ai pensé au TAF mais la fonction f' n est pas supposé continue pour conclure
des idées svp,?mrc d 'avance!
Dérivabilté
10 messages
- Page 1 sur 1
Re: dérivabilté
aviateur a écrit:tu peux écrire en latex de façon que cela soit lisible?
pardon je ne maitrise pas encore le latex, qu est ce qui te parait illisible?
Re: dérivabilté
Salut,
f est dérivable en donc il existe une fonction
donc il existe une fonction  définie sur I dont la limite en
définie sur I dont la limite en  est nulle et telle que pour tout
est nulle et telle que pour tout  dans
dans 
-f(d)= (x-d) f'(d)+ (x-d) \epsilon(x))
En particulier, pour tout , on a :
, on a :
-f(b_n)=f(a_n)-f(d)+f(d)-f(b_n)= (a_n-b_n)f'(d)+(a_n-d)\epsilon(a_n)+(d-b_n)\epsilon(b_n))
En divisant par) :
:
-f(b_n)}{a_n-b_n}= f'(d)+\frac{a_n-d}{a_n-b_n}\epsilon(a_n) + \frac{d-b_n}{a_n-b_n}\epsilon(b_n))
En passant à la limite, on obtient le résultat.
Par exemple :
) tend vers 0 quand n tend vers +infini et
tend vers 0 quand n tend vers +infini et

car
f est dérivable en
En particulier, pour tout
En divisant par
En passant à la limite, on obtient le résultat.
Par exemple :
car
Modifié en dernier par Elias le 30 Jan 2018, 23:53, modifié 2 fois.
Pseudo modifié : anciennement Trident2.
Re: dérivabilté
Trident2 a écrit:Salut,
f est dérivable endonc il existe une fonction
définie sur I dont la limite en
est nulle et telle que pour tout
dans

En particulier, pour tout, on a :
En divisant par:
En passant à la limite, on obtient le résultat.
Par exemple :tend vers 0 quand n tend vers +infini et
qui tend bien vers 1.
Ceci étant valable si pour n assez grand, les a_n sont tous non nuls (car je divise par a_n)
Si ce n'est pas le cas, c'est que (a_n) est stationnaire à 0 (car cette suite est convergente) et donc en remplaçant a_n par 0 on obtient la même chose...
Salut,
je comprend pas le passage en rouge on a pas une forme indéterminée 0/0 non ?
Re: dérivabilté
En effet, je suis allé un peu vite !
On peut dire plutôt que :

car
On peut dire plutôt que :
car
Pseudo modifié : anciennement Trident2.
Re: dérivabilté
Ah oui et donc :
 |< | \epsilon(a_n)|)
et ça tend vers 0 quand n tend vers l'infini bien joué !
(j'étais parti avec la notation petit "o" mais en fait c'est mieux de reprendre ton raisonnement avec espilon)
et ça tend vers 0 quand n tend vers l'infini bien joué !
(j'étais parti avec la notation petit "o" mais en fait c'est mieux de reprendre ton raisonnement avec espilon)
Re: dérivabilté
Je reviens systématiquement à epsilon dans ces situations.
Et sinon, faut quand même aussi le faire pour l'autre terme puisque du coup c'est moins évident :
 car
car (numérateur et dénominateur négatifs)
(numérateur et dénominateur négatifs)
Et sinon, faut quand même aussi le faire pour l'autre terme puisque du coup c'est moins évident :
Pseudo modifié : anciennement Trident2.
Re: dérivabilté
Salut,
A mon avis, c'est pas bête de "rallonger" l'exercice avec les questions suivantes :
- Montrer que le résultat perdure, si on ne suppose pas que an<d<bn mais qu'on suppose que f' est continue.
- Montrer à l'aide d'un exemple que le résultat peut être faux si on ne suppose pas que an<d<bn ni que f' est continue.
A mon avis, c'est pas bête de "rallonger" l'exercice avec les questions suivantes :
- Montrer que le résultat perdure, si on ne suppose pas que an<d<bn mais qu'on suppose que f' est continue.
- Montrer à l'aide d'un exemple que le résultat peut être faux si on ne suppose pas que an<d<bn ni que f' est continue.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: dérivabilté
Salut,
en effet, je m'étais posé la question aussi de voir si le résultat persistait en enlevant des hypothèses. Du coup, en y réfléchissant :
On suppose que f ' est continue sur I et non simplement en d ?
Dans ce cas, on s'en sort avec le théorème des accroissements finis.
Le premier exemple (classique) qui me vient est le cas de la fonction f définie sur R par= x^2 sin( \frac{1}{x} )) si
si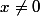 et
et=0)
On montre qu'elle est dérivable sur R et donc en particulier en 0 avec f '(0)=0. Mais sa dérivée n'est pas continue en 0.
En prenant les suites définies par et
et  , on montre par exemple que
, on montre par exemple que
-f(b_n)}{a_n-b_n} \rightarrow \frac{2}{\pi} \neq 0)
Mais il doit y avoir plus simple...
en effet, je m'étais posé la question aussi de voir si le résultat persistait en enlevant des hypothèses. Du coup, en y réfléchissant :
Ben314 a écrit:- Montrer que le résultat perdure, si on ne suppose pas que an<d<bn mais qu'on suppose que f' est continue.
On suppose que f ' est continue sur I et non simplement en d ?
Dans ce cas, on s'en sort avec le théorème des accroissements finis.
Ben314 a écrit:- Montrer à l'aide d'un exemple que le résultat peut être faux si on ne suppose pas que an<d<bn ni que f' est continue.
Le premier exemple (classique) qui me vient est le cas de la fonction f définie sur R par
On montre qu'elle est dérivable sur R et donc en particulier en 0 avec f '(0)=0. Mais sa dérivée n'est pas continue en 0.
En prenant les suites définies par
Mais il doit y avoir plus simple...
Pseudo modifié : anciennement Trident2.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
