Bonjour à tous,
Je bloque sur ce problème où il s'agit de démontrer la convergence ou la divergence de cette série en utilisant le test le plus adéquat (intégration, ratio,...) :
∑(de n=2 à l'infini) 1 / (n(ln(n) )^p * (ln(ln(n) ))^q ) Avec p>1 et q>1
Quelqu'un aurait-il une idée ?
Merci d'avance !!
Tester la concergence ou la divergence d'une série
10 messages
- Page 1 sur 1
Tester la concergence ou la divergence d'une série
Modifié en dernier par mathieuh96 le 24 Sep 2016, 23:28, modifié 1 fois.
Re: Tester la concergence ou la divergence d'une série
Peut-être avec la règle de Cauchy..?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Tester la concergence ou la divergence d'une série
Lostounet a écrit:Peut-être avec la règle de Cauchy..?
La racine n-ième permet de simplifier le problème ici ?
Re: Tester la concergence ou la divergence d'une série
Le nombre de parenthèses ne semble pas correct.
Re: Tester la concergence ou la divergence d'une série
Bonsoir,
C'est une série à termes positifs à partir d'un certain rang, et son terme général est un^p}\right)) (du moins sous réserve d'un bon parenthésage de l'expression).
(du moins sous réserve d'un bon parenthésage de l'expression).
On utilise ensuite les séries de Bertrand si c'est connu, ou sinon une comparaison série-intégrale.
C'est une série à termes positifs à partir d'un certain rang, et son terme général est un
On utilise ensuite les séries de Bertrand si c'est connu, ou sinon une comparaison série-intégrale.
Re: Tester la concergence ou la divergence d'une série
samoufar a écrit:Bonsoir,
C'est une série à termes positifs à partir d'un certain rang, et son terme général est un(du moins sous réserve d'un bon parenthésage de l'expression).
On utilise ensuite les séries de Bertrand si c'est connu, ou sinon une comparaison série-intégrale.
Désolé pour le parenthésage, je viens de la modifier. Du coup si je comprend bien, on ne tiens pas compte du terme (ln(ln(n)))^q ?
Re: Tester la concergence ou la divergence d'une série
Salut,
Si, tu sera obligé de tenir compte du 3em terme dans le cas où p=1 : c'est lui qui va déterminer si la série est convergente ou pas.
Indication : faire une comparaison Série/Intégrale et regarder ce que donne la dérivée de\Big)^\alpha) si
si  et de
et de )\Big)^\beta) si
si 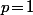 .
.
Si, tu sera obligé de tenir compte du 3em terme dans le cas où p=1 : c'est lui qui va déterminer si la série est convergente ou pas.
Indication : faire une comparaison Série/Intégrale et regarder ce que donne la dérivée de
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Tester la concergence ou la divergence d'une série
Bonsoir,
Sauf erreur, l'énoncé indique que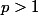 et
et 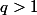 .
.
Ben314 a écrit:Salut,
Si, tu sera obligé de tenir compte du 3em terme dans le cas où p=1 : c'est lui qui va déterminer si la série est convergente ou pas.
Sauf erreur, l'énoncé indique que
Re: Tester la concergence ou la divergence d'une série
samoufar a écrit:Bonsoir,Ben314 a écrit:Salut,
Si, tu sera obligé de tenir compte du 3em terme dans le cas où p=1 : c'est lui qui va déterminer si la série est convergente ou pas.
Sauf erreur, l'énoncé indique queet
.
Oui c'est cela, p et q sont supérieurs à 1.
Je suis toujours perdu concernant le moyen de procéder...
Re: Tester la concergence ou la divergence d'une série
Ca fait deux fois qu'on te le dit : faire une comparaison Série/Intégrale.
Tu as jamais vu ça ?
Tu as jamais vu ça ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
