Correction Série

[sandrine_guillerme]

Salut tout le monde

1/

là j'ai dis que la suite des sommes partielles est bornée car suite géométrique de somme égale
et l'application décroissante vers 0 :
Le théorème d'Abel s'applique donc la série converge .



2/

la c'est pareil pour mais pour il n y a t il pas de méthode ou astuce intelligente a part étudier la fonction pour dire qu'elle décroit vers 0 (afin d'appliquer Abel bien sur ?)

4/ et sont équivalente ? elles sont de même nature ?
Pour l'équivalence j'ai appliquer la définition il faut prouver mais je ne vois pas le n'
:triste:
je sais qu'ils ont la même limite mais je ne vois pas du tout comment faire ! :triste:


Aidez moi? :triste:
Aidez moi svp? :triste:

Merci :triste:

[Quidam]

1/

A condition que et que z différent de 1.

et l'application décroissante vers 0

Plutôt : et l'application décroissante vers 0

il n y a t il pas de méthode ou astuce intelligente a part étudier la fonction pour dire qu'elle décroit vers 0

Ben, si tan(x) est équivalent à x
Donc si alors et est donc équivalent à

et

Ces deux suites ne sont pas équivalentes ! Mais qu'entends-tu par "de même nature" ?

[sandrine_guillerme]

Merci pour tes réponses eh oui pr ln je m'etais trompée .;

Sinan

Ces deux suites ne sont pas équivalentes ! Mais qu'entends-tu par "de même nature" ?

pourquoi tu dis qu'elle ne le sont pas???? pourtant moi je vois le contraire (coté intuitition quoi) mais si tu pourrais m'eclaircir ça serais gentil..
et quand je dis qu'elle sont de même nature ça veut dire soit elle convergent les deux ou bien diverge !

Merci beaucoup de me guider !!

[nuage]

Salut,

pourquoi tu dis qu'elle ne le sont pas???? pourtant moi je vois le contraire (coté intuitition quoi) mais si tu pourrais m'eclaircir ça serais gentil..
et quand je dis qu'elle sont de même nature ça veut dire soit elle convergent les deux ou bien diverge !

Merci beaucoup de me guider !!

Je n'ai pas étudié les séries que tu proposes, mais pour guider l'intuition tu peux comparer la nature des séries de terme général (convergente) et .

A+

[sandrine_guillerme]

salut nuage .. :triste:
mais je ne suis pas convaincu tu as majoré e/racine(n) par 1/n^2 Mais pourquoi? .. Et ça nous permettra de conclure quoi?

[Quidam]

Merci pour tes réponses eh oui pr ln je m'etais trompée .;

Sinan

pourquoi tu dis qu'elle ne le sont pas???? pourtant moi je vois le contraire (coté intuitition quoi) mais si tu pourrais m'eclaircir ça serais gentil..
et quand je dis qu'elle sont de même nature ça veut dire soit elle convergent les deux ou bien diverge !

Merci beaucoup de me guider !!

Elles convergent toutes deux vers 0 : je pense que c'est quasiment évident, tu es d'accord ?

Par contre on dit qu'elles sont équivalentes lorsque leur rapport tend vers 1, et là aussi, ce ne peut être le cas, car le rapport de la deuxième à la première peut certes s'approcher de 1 très près, mais il n'est borné par aucune constante, il peut arriver qu'il soit plus grand que n'importe quel nombre fixé à l'avance...
Il me semble t'avoir vu écrire quelque chose à ce sujet dans un fil récent ; je ne suis pas intervenu car il y avait déjà pas mal de monde sur le fil... Mais l'équivalence de deux suites n'est pas mesuré par leur différence (tendant vers 0) mais plutôt vers leur rapport, qui doit tendre vers 1 !
Va voir sur wikipédia : c'est bien cela la définition !
Par exemple et tendent toutes deux vers l'infini lorsque n tend vers l'infini. Leur différence tend vers l'infini, mais elles sont tout de même équivalentes car leur rapport tend vers 1.
J'espère que cela va t'éclairer.

[Quidam]

Un doute me prend soudain à la lecture du post de nuage. Je parlais bien sûr des suites et que tu as mentionnées. Je n'ai pas eu le temps, (je n'y ai même pas pensé à vrai dire) de répondre pour les séries. Et j'ignore si les séries sont ou pas équivalentes !
A priori, il me semble que la série de terme général converge, et que la série de terme général est divergente, mais je n'ai pas eu le temps d'étudier cela à fond...

[Quidam]

Après une nuit de réflexion (!), je réalise que j'ai réellement répondu trop vite ! Je confirme donc d'une part que je parlais des suites et et que tu parlais des séries de termes généraux respectifs et . D'ailleurs, j'avais bien spécifié "les suites...", mais je pense que ce ne sont pas les suites qui t'intéressent ! Navré pour cette bévue !

Donc, en ce qui concerne les séries, je pense que la série de terme général est convergente, si n'est pas égal à . Cela se "voit" géométriquement, si l'on représente les valeurs des sommes partielles dans le plan complexe. Les points représentant les vont suivre une sorte de spirale de "rayon" de plus en plus petit...Malheureusement, ce n'est évidemment pas une démonstration et je n'ai pas encore trouvé comment le prouver. D'un autre côté, étant donné la divergence de la série 1/n, la convergence de la série de terme général (une fois que cela sera prouvé) aura pour conséquence immédiate la divergence de la série de terme général : il suffira d'écrire les sommes partielles pour s'en convaincre.

[sandrine_guillerme]

Donc, en ce qui concerne les séries, je pense que la série de terme général est convergente, si n'est pas égal à . Cela se "voit" géométriquement, si l'on représente les valeurs des sommes partielles dans le plan complexe. Les points représentant les vont suivre une sorte de spirale de "rayon" de plus en plus petit.

Tu peux me dire tu l'a taper sous quel logiciel? je travaille sur Maple ou Scilab ça serais sympa de me donner la commande pour ldessiner la courbe ?

(...)Malheureusement, ce n'est évidemment pas une démonstration et je n'ai pas encore trouvé comment le prouver. D'un autre côté, étant donné la divergence de la série 1/n, la convergence de la série de terme général (une fois que cela sera prouvé) aura pour conséquence immédiate la divergence de la série de terme général : il suffira d'écrire les sommes partielles pour s'en convaincre.

Je crois que c'est bon je l'ai trouvé .. j'ai appliquer le critère D'Abel .. car la suite des somme partielle e^{in\theta} est borné et frac({1}{sqrt(n)} est décroissante vers 0 (bien sur on va pas étudier les series en tant que tel mais on va tout simplement faire l'etude d'une séries de fonction .. donc la séries converge ! :id:

[Quidam]

Tu peux me dire tu l'a taper sous quel logiciel? je travaille sur Maple ou Scilab ça serais sympa de me donner la commande pour ldessiner la courbe ?

Le logiciel le plus rapide du monde : conception, écriture, mise au point, exécution et visualisation des résultats : tout compris cinq secondes ! :ptdr: :ptdr: :ptdr:
C'est dans la tête que j'ai fait ça ! Je n'ai pas dessiné la courbe, je l'ai visualisée en regardant au loin l'horizon...En fait, il est facile d'imaginer les points qui se trouvent sur le cercle de centre O et de rayon unité, avec des angles successifs qui les séparent...Ensuite, j'imagine les mettre bout à bout, pour voir à quoi ressemblent les sommes partielles : ça va faire une sorte de polygone régulier...qui n'en est d'ailleurs pas un dans le cas général où est irrationnel. Enfin j'applique le facteur qui a pour effet de rapetisser chaque côté de plus en plus...D'où l'idée que ça doit faire une spirale...

Mais si tu veux, je peux te la dessiner aussi, en C++ (Maple, Scilab, connait pas !) !

[sandrine_guillerme]

Le logiciel le plus rapide du monde : conception, écriture, mise au point, exécution et visualisation des résultats : tout compris cinq secondes ! :ptdr: :ptdr: :ptdr:
C'est dans la tête que j'ai fait ça ! Je n'ai pas dessiné la courbe, je l'ai visualisée en regardant au loin l'horizon...En fait, il est facile d'imaginer les points qui se trouvent sur le cercle de centre O et de rayon unité, avec des angles successifs qui les séparent...Ensuite, j'imagine les mettre bout à bout, pour voir à quoi ressemblent les sommes partielles : ça va faire une sorte de polygone régulier...qui n'en est d'ailleurs pas un dans le cas général où est irrationnel. Enfin j'applique le facteur qui a pour effet de rapetisser chaque côté de plus en plus...D'où l'idée que ça doit faire une spirale...

Mais si tu veux, je peux te la dessiner aussi, en C++ (Maple, Scilab, connait pas !) !

Tu as de la chance moi .. mouarf.. jarrive pas a voir comment on pourrais faire niveau dessin .. j'aimerais bien l'avoir un jour .. parceque dans ce cas la, la moitié des probleme que j'ai en tete en analyse seront résolus.. c'est pour ça que je t'ai demander de ma le désssiner .. et donc ça serais gentil de le faire quand même tu peux le faire avec C++ l'essentiel c'est de voir une courbe réelle ..

Ensuite tu as dis qu'il est facile d'imaginer les points qui se trouvent sur le cercle de centre O et de rayon unité, ça oui je suis bien d'accord ..
mais "avec des angles successifs qui les séparent" je comprends pas ça ?? et pour le reste c'est bon j'ai compris ..

[Quidam]

Ensuite tu as dis qu'il est facile d'imaginer les points qui se trouvent sur le cercle de centre O et de rayon unité, ça oui je suis bien d'accord ..
mais "avec des angles successifs qui les séparent" je comprends pas ça ?? et pour le reste c'est bon j'ai compris ..

Ben oui, si est le point d'affixe , tu as :



etc et par conséquent :





non ?

Je vais voir si je peux faire ton dessin rapidement ! Mais, ça sera peut-être pas pour ce soir, demain sûrement (si je n'ai pas trop présumé de mes forces) !

[sandrine_guillerme]

ça y est maintenant j'ai compris cette histoire de exponentielle .. et je vois mieux que la somme partielle de la série de terme général on est bien d'accord .. et avec la somme partielle de la série de terme général quand rajoute la ça m'intrigue un petit peu ..

ce qui serait bien judicieux (et d'aileurs grandement apprècié) c'est de me faire le dessin des deux termes et en suite quand la somme et que ce que ça va donner .. et il n y a aucun soucie .. j'attendrais la réponse demain .. il me tarde (surement parceque c'est assez passionant ) vivement demain :zen:

Merci

[Quidam]

Voici deux images, où j'ai tracé (et relié) les points correspondant aux sommes partielles de 1 à n : l'une avec n=30, l'autre avec n=1000
Dans les deux cas
Il faut cliquer un coup pour avoir une image à la taille de l'écran, mais sauf si tu as un écran gigantesque, ce ne sera pas la bonne taille (comme les traits font 1 pixel de large, beaucoup de traits disparaissent lors de l'affichage forcé à la taille de ton écran). N'oublie pas de cliquer à nouveau sur l'image à la taille de l'écran pour avoir une image à la taille originelle (grande), prévue pour une impression sur papier A4.

[sandrine_guillerme]

D'accord maintenant au niveai du déssin je crois que j'ai bien compris.. passant maintenant a la démonstration rigoureuse.. je t'ai déja montré que les deux séries du termes générale.. sont équivalente.. mais il me semble que tu m'avais dis que les deux suites ne le sont pas.. pourquoi?
Merci

[Quidam]

là j'ai dis que la suite des sommes partielles est bornée car suite géométrique de somme égale
et l'application décroissante vers 0 :
Le théorème d'Abel s'applique donc la série converge .

Euh, panne de neurone, je ne me souvenais plus du théorème d'Abel. Un petit coup d'oeil à Wikipedia (http://fr.wikipedia.org/wiki/Th%C3%A9or%C3%A8me_d%27Abel_%28analyse%29) et je trouve un "théorème d'Abel" !
Je suppose que ce n'est pas de ce théorème-là que tu parles, car dans wikipédia les hypothèses ne sont pas ce que tu as démontré et la conclusion n'est pas non plus la tienne ! Peux-tu rafraîchir ma mémoire ?
Plus particulièrement, on ne dit pas "la série converge" lorsqu'il s'agit d'une série entière : en principe, ça dépend de z ! On parle de rayon de convergence, qui peut être fini, ou infini, certes, mais... Bref, je n'ai pas compris ce que tu as dit...

[Quidam]

je t'ai déja montré que les deux séries du termes générale.. sont équivalente

Où ça ?
Moi, je vois que tu as posé la question :

et sont équivalente ?

Mais je ne vois pas ni la réponse, ni la démonstration de cette absente réponse !

Pour l'équivalence j'ai appliquer la définition il faut prouver mais je ne vois pas le n'

Merci d'expliciter un peu...


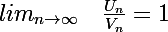
En outre, je ne sais pas ce que c'est que deux séries équivalentes ! Je sais que deux fonctions f et g sont équivalentes au voisinage de l'infini si . Je sais que deux suites U et V sont équivalentes au voisinage de l'infini si . Mais pour deux séries ... (c'est d'ailleurs pour cette raison que je me suis fourvoyé hier en raisonnant sur les suites et pas sur les séries !). Parles-tu des suites associées ? C'est à dire des suites des sommes partielles ?
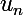
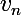
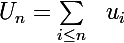
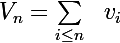
Dit-on que deux séries de termes généraux et sont équivalentes lorsque les suites et le sont ?

mais il me semble que tu m'avais dis que les deux suites ne le sont pas.. pourquoi?

Bien ! Revenons donc aux suites. Là, c'est moi qui ait fait erreur ! Navré d'avoir introduit le doute dans ton esprit ! J'aurais dû prendre la peine de prendre un crayon et un papier...Elles sont effectivement équivalentes :





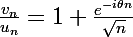
qui tend clairement vers 1 !
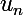
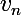
Cela dit, l'équivalence des suites et ne me semble pas impliquer l'équivalence des séries (au sens que j'ai supposé ci-dessus) sauf s'il y avait un autre théorème que j'aurais oublié également (je commence à avoir des doutes à présent :hum:). Car je n'ai pas (encore !) abandonné mon affirmation d'hier (à 9H06) :

selon laquelle les sommes partielles peuvent être décomposées en un partie qui converge et une autre qui diverge.
En d'autres termes : la série de terme général converge et la série de terme général
diverge. Euh..., enfin, jusqu'à ce que tu me montres le contraire !

[sandrine_guillerme]

Il me semble t'avoir vu écrire quelque chose à ce sujet dans un fil récent ; je ne suis pas intervenu car il y avait déjà pas mal de monde sur le fil... Mais l'équivalence de deux suites n'est pas mesuré par leur différence (tendant vers 0) mais plutôt vers leur rapport, qui doit tendre vers 1 !

ah nan je n'est jamais dis ça , mais petu etre si j'ai parler de différence de deux suite pour prouver l'équivalence c'est en utilisant la définition qu'est la suivante :


c'est la définition correcte et rigoureuse et pour la caractérisation des deux suites equivalente Oui dans ce cas la je suis bien d'accord la LIMITE de leur rapport, qui doit tendre vers 1 et ce n'est pas forcément EGAL A 1 !

Je crois que c'est bon je l'ai trouvé .. j'ai appliquer le critère D'Abel .. car la suite des somme partielle est borné et est décroissante vers 0 (bien sur on va pas étudier les series en tant que tel mais on va tout simplement faire l'etude d'une séries de fonction .. donc la séries converge !

et j'en profite pour te raffraichir la mémoire en te rappelant du critère d'Abel : et appelé aussi la forme réduite du théorème d'Abel
une série numérique si :
1/ la suite des sommes partielles de la série de terme général U_n est bornée
2/ décroissante vers 0

Donc la série converge

Pour l'équivalence j'ai appliquer la définition il faut prouver mais je ne vois pas le n'!

c'est en appliquant la définition de l'équivalence celle que j'ai noté en haut avec la notation "epsilonesque" et le probleme c'est de trouver le rang

En d'autres termes : la série de terme général converge et la série de terme général
diverge. Euh..., enfin, jusqu'à ce que tu me montres le contraire !

Ah oui c'est clair mais je ne sais pas pourquoi je sens qu'elle converge :hum:

En tout cas j'espère que j'étais assez claire (?) mais je ne vois toujours pas la réponse :--:

[Quidam]

Merci pour le critère d'Abel ; je l'avais oublié !

Oui dans ce cas la je suis bien d'accord la LIMITE de leur rapport, qui doit tendre vers 1 et ce n'est pas forcément EGAL A 1

Je ne comprend pas cette phrase. Je pense que la limite de leur rapport est égale à 1, c'est-à-dire que leur rapport tend vers 1. Je ne sais pas ce que tu as voulu dire ici.

En tout cas j'espère que j'étais assez claire (?) mais je ne vois toujours pas la réponse

Ben non, ce n'est pas très clair.

Persiste tu à penser que les deux séries convergent ?
Cela voudrait dire que tu n'est pas d'accord avec moi quand je dis :
"la série de terme général converge et la série de terme général
diverge."
Si tu as besoin d'une preuve...N'hésite pas !

[sandrine_guillerme]

ce que j'ai voulu dire par la limite de leur rapport , c'est qu'il tendent vers la même limite quoi .. je crois qu'on est bien d'accord finalement c'est cool :zen:
et j'ai une bonne nouvelle .. je comprends bien

En résumé :

les deux séries sont équivalentes la première est convergente et la deuxieme est divergente ..

sinon je vais te paraître un pe bête et soulante mais mon souhait c'est que tu m'explique encore plus le truc de dessin ça m'échape vraiment .. petit à petit stp .. et sache que je suis maintenant entièrement convaincu concernant la convergence et la divergence ! c'est cool c'est cool //

Une dernière question .. j'aurai bien aimé que tu me donne le code que tu as taper pour traçer les deux fonctions .. sur C++ je veux améliorer un peu mes connaissances concernant les dessins