Math Complexe et Logarithme
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 13 Avr 2016, 20:24
par Lostounet » 13 Avr 2016, 20:24
Voici:

D'une part:
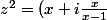^2 = x^2 + 2xi \frac{x}{x-1} - (\frac{x}{x-1})^2)
D'autre part:
z = (2 + 2i)(x+ i \frac{x}{x-1})= 2x + 2i \frac{x}{x-1} + 2ix - 2\frac{x}{x-1})
Donc, z^2 - (2+2i)z vaut:
^2 - 2x - 2i\frac{x}{x-1} - 2ix + 2\frac{x}{x-1})
Soit en réduisant la partie imaginaire au même dénominateur:
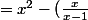^2 - 2x + 2\frac{x}{x-1} + i [ \frac{2x^2-2x-2x(x-1)}{x-1}])
Et donc la partie imaginaire est...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
LaylaManga
- Membre Naturel
- Messages: 76
- Enregistré le: 25 Oct 2014, 15:49
-
 par LaylaManga » 14 Avr 2016, 11:55
par LaylaManga » 14 Avr 2016, 11:55
Ah oui en effet, j'ai bien fait une erreur de calcul x') Merci beaucoup, je regarderais ce soir là je ne peux pas faire de math! ^^"
-
LaylaManga
- Membre Naturel
- Messages: 76
- Enregistré le: 25 Oct 2014, 15:49
-
 par LaylaManga » 15 Avr 2016, 08:54
par LaylaManga » 15 Avr 2016, 08:54
J'ai encore un service à vous demander....
C'est pour l'exercice 3, pour la a), j'ai bien réussi à trouver x'=(x²-y²)/(x²+y²) mais pour y' je ne sais pas si je dois repartir du z'=(z/|z|)² ou si je dois reprendre le x'... J'ai essayé de faire z'=x'+yi'
z'=x²-y²+2yi' <==>y'=(x²-y²+2i)/z' <==> y'=(x²-y²+2i)/x'+yi' mais après je revient sur un point de départ......
Pourriez-vous m'aider pour ça? Merci! ^^

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 15 Avr 2016, 11:54
par Lostounet » 15 Avr 2016, 11:54
Il vaut mieux partir du z' plutôt. Pourquoi tu bloques? C'est simple:
D'une part z^2=x^2-y^2+2ixy
D'autre part |z|=x^2+y^2
Il suffit donc de dire que z'= (x^2-y^2+2ixy)/(x^2+y^2)
Et donc x'=Re(z')=...
Y'=Im(z')=..
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
LaylaManga
- Membre Naturel
- Messages: 76
- Enregistré le: 25 Oct 2014, 15:49
-
 par LaylaManga » 15 Avr 2016, 18:20
par LaylaManga » 15 Avr 2016, 18:20
Euh juste.. dans l'expression il n'y a pas y'...
Et pour la b), je dois bien faire z'=(z/(|z|)², où je remplace z par x+yi et trouver à la fin pas de partie réelle mais qu'une partie imaginaire n'est-ce pas?

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 16 Avr 2016, 01:38
par Lostounet » 16 Avr 2016, 01:38
..? Qu'est-ce que tu veux dire... "il n'y a pas y' " ?
b) Oui, mais il faut faire proprement les choses
Dire que deux propositions P et Q sont équivalentes signifie que P implique Q ET
Q implique P
Il faudrait donc montrer que si P alors Q
Et aussi si Q alors P
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
LaylaManga
- Membre Naturel
- Messages: 76
- Enregistré le: 25 Oct 2014, 15:49
-
 par LaylaManga » 17 Avr 2016, 09:28
par LaylaManga » 17 Avr 2016, 09:28
Bonjour!
Je crois avoir résolu mon problème pour y' ^^
Mais sinon pour la b), le plus simple c'est de partir de quoi? Vous pouvez me donner un point de départ?!
Merci! ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités