Bonjour à tous !
Alors voila mon probleme: montrer que Pi/4=5arctan(1/7)+2arctan(3/79)..
Pas mal de personnes ont cherchés ce probleme, mais jusque la je n'ai vu personne reussir.
Ma premiere idée etait de passer a tan(Pi/4)=tan[ 5arctan(1/7)+2arctan(3/79) ]
Par tan(a+b)= [tan(a)+tan(b)]/ [1+tan(a)tan(b)] j'obtiens une nouvelle forme...
Mais voila ca fait des tan(5*arctan(1/7)) et tan(2arctan(3/79))....
S'il vous plait aidez moi, je sais vraiement pas quoi faire avec ca...
A tous merci beaucoup d'avance !!!
Pi/4=5arctan(1/7)+2arctan(3/79)
10 messages
- Page 1 sur 1
par thibo777 » 02 Oct 2006, 19:29
oui je n'avais jamais entendu parler de Machin, mais comment démontrer cette égalité ?
par Jacques COLLOT » 02 Oct 2006, 19:38
Cette formule a été trouvée par Euler en 1755
Voir
http://s146372241.onlinehome.fr/web/pi314.net/machin.php
Voir aussi dans "Le fascinant nombre pi" de Jean-Paul Delahaye un tas d'explications sur les démonstrations des formules d'arctan.
Jacques
Voir
http://s146372241.onlinehome.fr/web/pi314.net/machin.php
Voir aussi dans "Le fascinant nombre pi" de Jean-Paul Delahaye un tas d'explications sur les démonstrations des formules d'arctan.
Jacques
par thibo777 » 02 Oct 2006, 19:55
Oui c'est bien cela, j'avais d'ailleur aussi consulté cet excelent site sur Pi, mais ce que je n'ai jamais pu trouver c'est la démonstration de cette formule d'Euler...
par Jacques COLLOT » 04 Oct 2006, 11:17
Voici la solution
Cette méthode s'applique à la plupart des formules en arctan
Le début est repris du livre déjà mentionné plus haut.
Pour démontrer les formules de décomposition de pi/a en somme d'arc tangentes, la méthode la plus simple consiste à utiliser plusieurs fois de suite la relation
 = {{\tan a + \tan b} \over {1 + \tan a\tan b}})
Etablissons par exemple la formule suivante, qui étatit déjà connue d'Euler
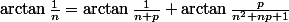
Pour cela, on calcule
)
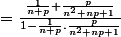
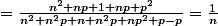
On par maintenant de pi/4 = arctan 1/1 , et on applique un ceratin nombre de fois la fomule ci-dessus. On aura successivement
Voilà j'espère que cela répond à la question.
Jacques
Cette méthode s'applique à la plupart des formules en arctan
Le début est repris du livre déjà mentionné plus haut.
Pour démontrer les formules de décomposition de pi/a en somme d'arc tangentes, la méthode la plus simple consiste à utiliser plusieurs fois de suite la relation
Etablissons par exemple la formule suivante, qui étatit déjà connue d'Euler
Pour cela, on calcule
On par maintenant de pi/4 = arctan 1/1 , et on applique un ceratin nombre de fois la fomule ci-dessus. On aura successivement
Voilà j'espère que cela répond à la question.
Jacques
!!
par hazal_kaya » 08 Oct 2014, 21:59
quelqu un peut m expliquer le passage de arctan 3/4 à arctan 1/7+arctan17/31 ??
par deltab » 09 Oct 2014, 01:19
Bonsoir.
On peut aussi s'en tirer en appliquant plusieurs fois la formule=\dfrac{\tan(a)+\tan(b)}{1-\tan(a)\tan(b)})
et non =\dfrac{\tan(a)+\tan(b)}{1+\tan(a)\tan(b)})
et son corollaire =\dfrac{2\tan(a)}{1-\tan^2(a)})
.
=\tan(4a+a)=\dfrac{\tan(4a)+\tan(a)}{1-\tan(4a)\tan(a)})
=\dfrac{2\tan(2a)}{1-\tan^2(2a)})
On peut ainsi exprimer))
comme fonction rationnelle de )=3/79)
(donc est rationnel). De même ))
est une fonction rationnelle de )=1/7)
. Il reste à récapituler et l'on devrait aboutir à:
)+2\arctan(3/79))=1)
PS: On a pour n entier naturel)
est une fonction rationnelle de )
On peut aussi s'en tirer en appliquant plusieurs fois la formule
On peut ainsi exprimer
PS: On a pour n entier naturel
par chan79 » 09 Oct 2014, 08:42
hazal_kaya a écrit:quelqu un peut m expliquer le passage de arctan 3/4 à arctan 1/7+arctan17/31 ??
salut
on cherche
on trouve
par hazal_kaya » 09 Oct 2014, 16:39
ah oui merci ..
peut on la demontrer en utilisant que :
arctan(a)-2arctan(b)=arctan((a-2b-ab²)/(1+2ab-b²))
que pensez vous??
peut on la demontrer en utilisant que :
arctan(a)-2arctan(b)=arctan((a-2b-ab²)/(1+2ab-b²))
que pensez vous??
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :