merci, j'ai vu et c'est très clair.
rq :
c'est le calcul de la dérive... de la fonction dérivée.
C'est noté.
[quote]====> en fait, le "calcul de la dériv
ée" c'est le calcul de la
pente de la tangente à la courbe, en tous points de cette dernière. Et la pente, c'est un rapport qui est =
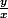
C'est pour cela que dans mon tableau, on a f'(x) >0 de -2 à -1 et de 1 à 2 (la tangente monte) et g(x)= -1
x -1.5 ==> g(x)= -0.125
x -1 ===> g(x)= 0.5
x 0 ====> g(x)= 1
x 0.5===> g(x)= 1.125
x 1 ====> g(x)= 1.5
x 1.5 ===> g(x)= 2.25
x 2 ====> g(x)= 3
Ensuite de construire graphiquement la courbe Cg de la fonction g. Je l'ai inséré dans le 1° schéma, c'est plus simple pour la suite.
[img][url=http://pix.toile-libre.org/?img=1443035523.png][img]http://pix.toile-libre.org/upload/img/1443035523.png[/img][/url[/IMG]
on me demande de résoudre graphiquement f(x)=g(x)... je ne comprend pas trop, il me semble que la courbe parle d'elle même (???)
de résoudre graphiquement que f(x)

g(x) . Idem (???)
le point A (5/4 ; 7/4) appartient-il à Cg ? ===> je répond non, mais je ne sais pas comment le justifier, même si je constate que ces points ne figure pas sur la courbe...
Et la cerise sur le gâteau: Démontrer par le calcul que la fonction g admet un minimum égal à 1 sur l'interval [-2 ; 2]...
Je ne vous demande pas de le faire à ma place, mais je cherche vraiment à comprendre comment...

Votre soutient et vos corrections sont les bienvenus.
Merci
