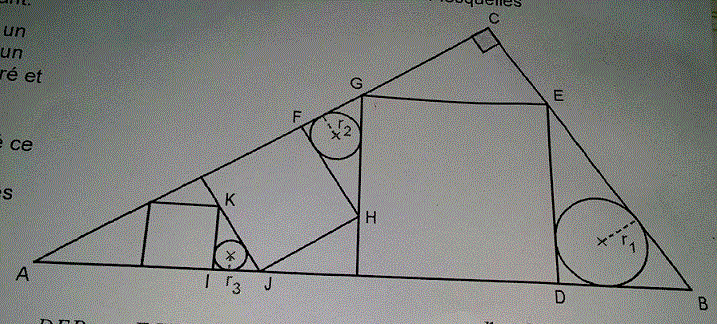
On se propose de résoudre le sangaku suivant:
Pour obtenir la figure ci-contre, on a dessiné un triangle rectangle ABC puis on y a inscrit un carré. Le triangle est donc découpé en un carré et trois triangles. Dans l'un des des triangles ne contenant pas le point C on a dessiné un cercle inscrit, et dans l'autre on a recommencé ce protocole. Après deux étapes, on a obtenu la figure ci-contre. On note r1, r2 et r3 les rayons respectifs des trois cercles obtenus.
Objectif: Démontrer que r1r3=r2
Indication:Que peut-on dire des triangles ABC, DEB, FGH et IJK ? En déduire que r1/r2=r2/r3 et conclure.
merci pour l'aide apporté