Barycente

[jiji59320]

bonjours encore moi,j'ai un exercice que sur les barycentre et le prof nous a pas encore donner le cours pourriez vous me donner un ptit coup de pouce.

le plan etant muni d'un repere d'origine 0,soient les points A=(2,4) et C(6,0).soient B' et K les milieux respectif de (AC) et (OB').
1°calculer les coordonnées de B' et K.
2°soit I=(2,0) trouver les reels a et b tels que K soit le barycentre de (A,a)(I,b)
3°calculer les coordonnées du barycentre J de (A,1)(O,2)
4°prouver que (IJ) parallele a (AC).

merci

[c pi]

Bonsoir

A la première question il s'agit simplement des coordonnées de milieux.

Au collège on apprend qu'il suffit de calculer la demi-somme des coordonnées des extrémités.

[jiji59320]

salut,ça j'ai reussi mais c'est apres que je n'y arrive pas.

rep

[Flodelarab]

salut,ça j'ai reussi mais c'est apres que je n'y arrive pas.

rep

Quelque soit le point M du plan, de coordonnées (x,y), on peut écrire:
si la somme des poids est différents de 0 et que K est le barycentre des points A de poids a et I de poids b

[jiji59320]

euh et apres cela tu fais comment pour trouver a et b...,

merci d'avance

[Flodelarab]

euh et apres cela tu fais comment pour trouver a et b...,

merci d'avance

Combien d'inconnues ? Combien d'équations ?

[c pi]

Bonjour

si la somme des poids est différents de 0 et que K est le barycentre des points A de poids a et I de poids b

Pour réduire le nombre des inconnues,
je me permets d'intervenir en adaptant cette relation générale
au cas particulier où le point M = K

[Flodelarab]

Bonjour


Pour réduire le nombre des inconnues,
je me permets d'intervenir en adaptant cette relation générale
au cas particulier où le point M = K

Ohhhh intéressant.
Moi, j'aurais plutot choisis M=O de coordonnées (0,0) ...
Chacun fait fait fait ce qui lui plait plait plait

[c pi]

Moi, j'aurais plutot choisis M=O de coordonnées (0,0) ...

OK Flodelarab,
ton O est plus pure que mon K !

C'était juste pour faire avancer le schmilblicK...

[rene38]

Salut

OK Flodelarab,
ton O est plus pure que mon K !

C'était juste pour faire avancer le schmilblicK...

C'est quoi, cette histoire de tonneau ?

[jiji59320]

et apres ça comment je fait pour calculer a et b,je n'ai pas encore fait le cours je ne sais pas dutt le faire.

et par contre pour la 3eme question je trouve (2,4) mais c'est impossible car kan je le place sur le plan ca ne fait pas dutt parallele a ac alors qu'il nous demande dans la derniere question de le prouver.

j'ai du fair une betise quelque par.

aider moi merci d'avance.

[euclide]

On peut aussi utiliser les nombres complexes :



on connait et on prend une valeur arbitraire de a par exemple 1 et on en déduit la valeur correspondante de b pour cette valeur de a (je rappelle que le couple (a;b) n'est pas unique ).

Dans ce cas on trouve a = 1 et b = 3.

[euclide]

Avec le recule je me suis dit que la méthode des nombres comlexes n'était peut être pas adéquate parce-que tu ne l'as peut être pas encore vu donc j'ai une autre méthode.

Comme il a été dit précedement on a :

a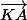 + b =

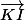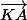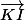et en utilisant la relation de Chasles on peut remplacer et par :

= +
= +

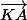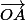
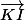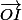
où O est l'origine du repère. On a donc :

a( + 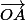) + b( + ) =

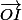Et là il n'y a que des choses qu'on connait :

= -

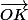
donc on a :

a(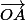-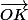) + b(-) =

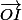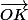ensuite on peut remplacer par les coordonnées :

=
=
=
=

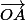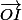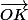d'où :

a(-) + b(-) =

en développant on a :

+ =

+ =

=

Donc on trouve léquation :

3a-b = 0
b=3a

Conclusion : Toutes les valeurs de a et b qui vérifient cette équation (b=3a) sont des valeurs qui marchent par exemle a=1 et b=3 ou a=2 et b=6 etc.

PS : S'il y a quelque chose que tu n'as pas compris ou si la méthode ne satisfait pas n'hésite pas à le dire il y a de trés nombreuses façon de résoudre le problème.

[jiji59320]

merci c'est tres gentil de ta part de m'avoir aidé.ne t'inquite pas j'ai tout a fait compris ta methode.
mais maintenant comment tu fait pour les 2 question suivante.dsl de t'embeter.
meric bcp.

[Flodelarab]

Avec le recule je me suis dit que la méthode des nombres comlexes n'était peut être pas adéquate parce-que tu ne l'as peut être pas encore vu donc j'ai une autre méthode.

Comme il a été dit précedement on a :

a + b =

et en utilisant la relation de Chasles on peut remplacer et par :

= +
= +

où O est l'origine du repère. On a donc :

a( + ) + b( + ) =

Et là il n'y a que des choses qu'on connait :

= -

donc on a :

a(-) + b(-) =

ensuite on peut remplacer par les coordonnées :

=
=
=
=

d'où :

a(-) + b(-) =

en développant on a :

+ =

+ =

=

Donc on trouve léquation :

3a-b = 0
b=3a

Conclusion : Toutes les valeurs de a et b qui vérifient cette équation (b=3a) sont des valeurs qui marchent par exemle a=1 et b=3 ou a=2 et b=6 etc.

PS : S'il y a quelque chose que tu n'as pas compris ou si la méthode ne satisfait pas n'hésite pas à le dire il y a de trés nombreuses façon de résoudre le problème.

Je suis surpris du nombres de circonvolutions que tu fais avant d'atteindre ton but.

1. Les complexes : regrouper n'est pas résoudre.
2. vecteurs KA et KI connu : pas besoin de Chasles
3. vecteurs OK OA OI directement utilisable si M=O : pas besoin de Chasles

[jiji59320]

explique ta solution pour voir si tu trouve vraiment pareil stp merci.

[euclide]

D'abord en réponse à "flodelarab", j'ai préféré tout détailler et c'est par choix il n'y a pas d'erreurs dand mon raisonnement y compris pour les nombres complexes j'ai juste pas tout dévéloppé pour ce cas. Peut être qu'il y en a de plus simles c'est vrai mais bon ca marche.

Pour les question suivantes :

Pour calculer le barycentre J de (A,1)(O,2) il faut utiliser la même formule :

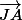+2 =

Si on prend comme coordonnées de J :

on a:

=
=

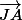d'où :

+2=

Ensuite tu développe comme dans la question précedente et tu en déduis les coordonnées recherchées.

Et pour la question 4 il faut que tu montre que les vecteurs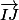 et sont colinéaires.

[jiji59320]

je suis dsl mais je n'est pas compris la 3eme question comment tu fait pour trouver les coordonnées.je ne voi pas dutout.
tu peux m'aider stp merci d'avance.
+

[euclide]

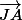On cherche le coordonnées de J, elles sont de la forme J= tu connais les coordonnées des points O (l'origine) et A donc tu peux calculer les coordonnées des vecteurs et . On sait que J est le barycentre de (A,1) et (O,2) donc on a cette formule :

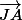+2=

Ensuite tu remplaces dans cette formule les vecteurs par leurs coordonnées et tu as :

+ 2 =
=
=

d'où le système :



aprés tu résouds le système et tu déduit les valeurs de a et b qui sont les coordonnée de J (J=).

[jiji59320]

ok ca y est merci c'est trop sympas et gentil de ta part.
tu n'aurait pas une adresse msn pour que la prochaine fois je puisse te demander par mail des question.
t'inquiete je ne vais pas tout les jours te donner des exo a faire .lol.
nn mais c'est juste comme ca dit moi quoi et merci encore.