Exercice sur les fonctions [2nd]
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mathelot
 par mathelot » 11 Fév 2015, 17:06
par mathelot » 11 Fév 2015, 17:06
elevedeseconde a écrit:donc, MN² = x² - 1
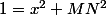
on soustraie

de chaque côté de l'égalité.
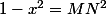
l'égalité est symétrique
si a=b alors b=a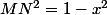
-
elevedeseconde
- Membre Relatif
- Messages: 205
- Enregistré le: 11 Fév 2015, 15:34
-
 par elevedeseconde » 11 Fév 2015, 17:10
par elevedeseconde » 11 Fév 2015, 17:10
Ok, merci mais pour le 3) je ne comprends pas du tout O_o
-
mathelot
 par mathelot » 11 Fév 2015, 17:14
par mathelot » 11 Fév 2015, 17:14
je dois m'en aller...
-
elevedeseconde
- Membre Relatif
- Messages: 205
- Enregistré le: 11 Fév 2015, 15:34
-
 par elevedeseconde » 11 Fév 2015, 17:15
par elevedeseconde » 11 Fév 2015, 17:15
ok, merci encore, ,sinon tu reviendras plus tard ?
si quelqu'un d'autre pourrait m'aider ca serait cool =)
-
elevedeseconde
- Membre Relatif
- Messages: 205
- Enregistré le: 11 Fév 2015, 15:34
-
 par elevedeseconde » 11 Fév 2015, 18:11
par elevedeseconde » 11 Fév 2015, 18:11
elevedeseconde a écrit:ok, merci encore, ,sinon tu reviendras plus tard ?
si quelqu'un d'autre pourrait m'aider ca serait cool =)
vraiment cool.. :'(
-
mathelot
 par mathelot » 11 Fév 2015, 18:15
par mathelot » 11 Fév 2015, 18:15
un triangle rectangle est la moitié d'un rectangle
(on peut justifier cette affirmation avec une symétrie centrale)
Quelle est donc la formule d'aire d'une moitié de rectangle ??
-
elevedeseconde
- Membre Relatif
- Messages: 205
- Enregistré le: 11 Fév 2015, 15:34
-
 par elevedeseconde » 11 Fév 2015, 18:32
par elevedeseconde » 11 Fév 2015, 18:32
Non mais j'me suis trompé, en écrivant l'énoncé c'est
3) Retrouver alors l'expression de f(x) = x/2 racine carré de 1- x au carré
Doit-on remplacera x par 1 ? Si c'est cela, alors ça fait 0.
-
elevedeseconde
- Membre Relatif
- Messages: 205
- Enregistré le: 11 Fév 2015, 15:34
-
 par elevedeseconde » 11 Fév 2015, 19:19
par elevedeseconde » 11 Fév 2015, 19:19
Si quelqu'un pourrait m'aider parce-que ça fait un peu plus d'1h que j'attends merci d'avance
-
mathelot
 par mathelot » 11 Fév 2015, 22:15
par mathelot » 11 Fév 2015, 22:15
l'aire du triangle AMN est

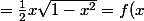)
Comme il y a une racine, on travaille avec
)
dans les questions suivantes,
car
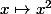
est strictement croissante sur R+, et donc conserve les extrema
entre
)
et
)
^2 =\max_{x \in [0;1]} (f^2))
-
mathelot
 par mathelot » 11 Fév 2015, 22:53
par mathelot » 11 Fév 2015, 22:53
télécharger CarMetal ou Geogebra pour faire de jolis dessins.
-
elevedeseconde
- Membre Relatif
- Messages: 205
- Enregistré le: 11 Fév 2015, 15:34
-
 par elevedeseconde » 11 Fév 2015, 22:59
par elevedeseconde » 11 Fév 2015, 22:59
ok merci pour la 3) on développe donc,
(f(x))²-(1/4)² = x²-(1-x²) / 4 - 1/16
= 4x²(1-x²)-1 / 16
= 4x²-4x-1 / 16 ?
-
mathelot
 par mathelot » 11 Fév 2015, 23:29
par mathelot » 11 Fév 2015, 23:29
=\frac{x^2 (1-x^2)}{4}- \frac{1}{16})
développe et factorise par
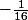
-
elevedeseconde
- Membre Relatif
- Messages: 205
- Enregistré le: 11 Fév 2015, 15:34
-
 par elevedeseconde » 11 Fév 2015, 23:39
par elevedeseconde » 11 Fév 2015, 23:39
j'pense pas réussir à l'faire j'suis trop nul, si on passait à la 5 stp merci d'avance et beaucoup
-
mathelot
 par mathelot » 11 Fév 2015, 23:45
par mathelot » 11 Fév 2015, 23:45
-\frac{1}{16}=\frac{x^2 (1-x^2)}{4}- \frac{1}{16})
réduction au même dénominateur
-\frac{1}{16}=\frac{4x^2 (1-x^2)}{16}- \frac{1}{16})
on commence par factoriser 1/16
-\frac{1}{16}=\frac{1}{16} \left( 4x^2 (1-x^2)-1 \right))
peux tu terminer ? il faut développer et factoriser par -1 en changeant le
signe de chaque terme

-
elevedeseconde
- Membre Relatif
- Messages: 205
- Enregistré le: 11 Fév 2015, 15:34
-
 par elevedeseconde » 11 Fév 2015, 23:52
par elevedeseconde » 11 Fév 2015, 23:52
Non désolé, mais j'comprends tes démarches.
-
elevedeseconde
- Membre Relatif
- Messages: 205
- Enregistré le: 11 Fév 2015, 15:34
-
 par elevedeseconde » 12 Fév 2015, 00:13
par elevedeseconde » 12 Fév 2015, 00:13
mathelo t la on fini ca rapidement en faisant le 5) et 6) comme ça j'pars me coucher
-
mathelot
 par mathelot » 12 Fév 2015, 00:15
par mathelot » 12 Fév 2015, 00:15
on commence par factoriser 1/16
^2-\frac{1}{16}=\frac{1}{16} \left( 4x^2 (1-x^2)-1 \right))
on développe à l'intérieur des grandes parenthèses
^2-\frac{1}{16}=\frac{1}{16} \left( 4x^2-4x^4-1 \right))
on factorise -1
^2-\frac{1}{16}=-\frac{1}{16} \left( -4x^2+4x^4+1 \right))
^2-\frac{1}{16}=-\frac{1}{16} \left( 4x^4 -4x^2+1 \right))
^2-\frac{1}{16}=-\frac{1}{16} \left( 4x^4 -4x^2+1 \right))
on reconnaît un carré parfait
^2-\frac{1}{16}=-\frac{1}{16} \left( 2x^2-1\right)^2)
^2=\frac{1}{16}-\frac{1}{16} \left( 2x^2-1\right)^2)
d'où
 \leq \frac{1}{16})
comme
 \geq 0)
à ce stade, on obtient:
 \leq \frac{1}{4} \qquad \forall x \in [0;1])
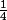
est un majorant de

comme
=\frac{1}{4})
1/4 est le maximum de f sur [0;1] atteint pour x=1/V2
-
elevedeseconde
- Membre Relatif
- Messages: 205
- Enregistré le: 11 Fév 2015, 15:34
-
 par elevedeseconde » 12 Fév 2015, 00:20
par elevedeseconde » 12 Fév 2015, 00:20
ok merci et pour le 6 f(racine carré de 2 ) /2 ) = 1/4 et pour conclure je dis?
-
mathelot
 par mathelot » 12 Fév 2015, 00:22
par mathelot » 12 Fév 2015, 00:22
elevedeseconde a écrit:ok merci et pour le 6 f(racine carré de 2 ) /2 ) = 1/4 et pour conclure je dis?
conclusion : 1/4 est le maximum de f sur [0;1] atteint pour x=1/V2
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités