Formule de changement de variables.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
EGA-SGA
- Membre Naturel
- Messages: 61
- Enregistré le: 03 Mai 2013, 16:10
-
 par EGA-SGA » 09 Jan 2015, 00:39
par EGA-SGA » 09 Jan 2015, 00:39
barbu23 a écrit:Je m'excuse, j'ai confondu avec l'algèbre symétrique, l'algèbre altérnée est plutot ça , non ? :
)
.
Oui, oui, bien sur.
Bon, peu importe. Merci pour ta réponse. Peux tu m'expliquer pourquoi :
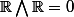
.
Ben répond à ma question posée plus haut
si V est un espace de dimension 1, et f une 2-forme alternée sur V... que vaut f(x,y)?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2015, 00:40
par barbu23 » 09 Jan 2015, 00:40
Ah d'accord, parce que :
 = xy f(1,1) = xy. 0 = 0)
.
-
EGA-SGA
- Membre Naturel
- Messages: 61
- Enregistré le: 03 Mai 2013, 16:10
-
 par EGA-SGA » 09 Jan 2015, 00:43
par EGA-SGA » 09 Jan 2015, 00:43
Et pourquoi donc f(1,1) vaudrait 0? Et qui est 1 dans un espace vectoriel de dimension 1 quelconque?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2015, 00:44
par barbu23 » 09 Jan 2015, 00:44
EGA-SGA a écrit:Y a pas d'analyse complexe ici. Le cercle est de dimension 1, donc
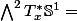
?
D'accord, donc, il n'y'a que la forme nulle qu'on peut intégrer sur un cercle, non ?
-
EGA-SGA
- Membre Naturel
- Messages: 61
- Enregistré le: 03 Mai 2013, 16:10
-
 par EGA-SGA » 09 Jan 2015, 00:45
par EGA-SGA » 09 Jan 2015, 00:45
barbu23 a écrit:D'accord, donc, il n'y'a que la forme nulle qu'on peut intégrer sur un cercle, non ?
Non.
Tu comptes juste balancer des trucs au hasard et tomber sur qqch de coherent? Peu de chance.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2015, 00:46
par barbu23 » 09 Jan 2015, 00:46
EGA-SGA a écrit:Et pourquoi donc f(1,1) vaudrait 0? Et qui est 1 dans un espace vectoriel de dimension 1 quelconque?
 = xy f(e_1 , e_1 ) = xy.0 = 0)
.
Parce que la

- forme est alternée, non ? c'est un élément du fibré cotangent du cercle, non ?.
-
EGA-SGA
- Membre Naturel
- Messages: 61
- Enregistré le: 03 Mai 2013, 16:10
-
 par EGA-SGA » 09 Jan 2015, 00:49
par EGA-SGA » 09 Jan 2015, 00:49
barbu23 a écrit: = xy f(e_1 , e_1 ) = xy.0 = 0)
.
C"est deja mieux. Et pourquoi f(e_1, e_1)=0 ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2015, 00:50
par barbu23 » 09 Jan 2015, 00:50
EGA-SGA a écrit:Non.
Tu comptes juste balancer des trucs au hasard et tomber sur qqch de coherent? Peu de chance.
Parce que, de manière générale, l'intégrale est définie ainsi :
 \to \mathbb{R})
, non ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2015, 00:52
par barbu23 » 09 Jan 2015, 00:52
EGA-SGA a écrit:C"est deja mieux. Et pourquoi f(e_1, e_1)=0 ?
Parce que
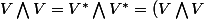^*)
donc, un élément de ce truc là, c'est une forme altérnée, non ?
-
EGA-SGA
- Membre Naturel
- Messages: 61
- Enregistré le: 03 Mai 2013, 16:10
-
 par EGA-SGA » 09 Jan 2015, 00:54
par EGA-SGA » 09 Jan 2015, 00:54
Mais, est ce que tu comprend ce que t'ecris...?
Oui, f est alternée, y a pas besoin de "prouver" ca, puisque on a pris f une 2-forme alternée...
si V est un espace de dimension 1, et f une 2-forme alternée sur V... que vaut f(x,y)?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2015, 00:57
par barbu23 » 09 Jan 2015, 00:57
EGA-SGA a écrit:Mais, est ce que tu comprend ce que t'ecris...?
Oui, f est alternée, y a pas besoin de "prouver" ca, puisque on a pris f une 2-forme alternée...
Oui, voilà. Tu me l'a déjà dit, il faut que je reprennes les bases. Mais, je ne comprends pas quant tu dis : Bon, deja des 2-formes sur le cercle, y en a pas beaucoup. UNe seule à vrai dire.
-
EGA-SGA
- Membre Naturel
- Messages: 61
- Enregistré le: 03 Mai 2013, 16:10
-
 par EGA-SGA » 09 Jan 2015, 00:59
par EGA-SGA » 09 Jan 2015, 00:59
Non, mais tu peux laisser tomber ca.
Essaie deja de comprendre pourquoi la seule 2-forme alternée sur un espace vectoriel de dimension 1 est nulle
(et du coup la seule 2 forme sur le cercle est nulle parce que l'espace tangent au cercle en un point quelconque est de dimension 1).
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2015, 01:04
par barbu23 » 09 Jan 2015, 01:04
EGA-SGA a écrit:Non, mais tu peux laisser tomber ca.
Essaie deja de comprendre pourquoi la seule 2-forme alternée sur un espace vectoriel de dimension 1 est nulle
(et du coup la seule 2 forme sur le cercle est nulle parce que l'espace tangent au cercle en un point quelconque est de dimension 1).
Le comprendre comment ? Intuitivement ? c'est à dire géométriquement ?, ou bien à travers ce qu'on a dit tout à l'heure :
 = xy f(e_1 , e_1 ) = 0)
?
-
EGA-SGA
- Membre Naturel
- Messages: 61
- Enregistré le: 03 Mai 2013, 16:10
-
 par EGA-SGA » 09 Jan 2015, 01:06
par EGA-SGA » 09 Jan 2015, 01:06
Ben deja en donner une démonstration... tu pretend que f(e_1, e_1)=0, mais peux tu donner un argument pour cela (c'est pas une question piege, hein) ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2015, 01:10
par barbu23 » 09 Jan 2015, 01:10
EGA-SGA a écrit:Ben deja en donner une démonstration... tu pretend que f(e_1, e_1)=0, mais peux tu donner un argument pour cela (c'est pas une question piege, hein) ?
 = e_1 \wedge e_1 = 0)
, non ?
-
EGA-SGA
- Membre Naturel
- Messages: 61
- Enregistré le: 03 Mai 2013, 16:10
-
 par EGA-SGA » 09 Jan 2015, 01:11
par EGA-SGA » 09 Jan 2015, 01:11
Laisse tomber. Vraiment.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2015, 01:13
par barbu23 » 09 Jan 2015, 01:13
EGA-SGA a écrit:Laisse tomber. Vraiment.
 = \wedge ( e_1 , e_1 ))
???
Peux tu me dire où est mon erreur ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2015, 01:16
par barbu23 » 09 Jan 2015, 01:16
Bonne nuit.
C'est juste ma propre interprétation que je sais à priori que c'est faux, mais moi, je cherche juste l'intuition derrière ce

qui vaut toujours

, c'est bizarre. :marteau:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2015, 01:41
par barbu23 » 09 Jan 2015, 01:41
Une dernière question :
Lorsqu'on veut intégrer une fonction

sur le cercle unité

, il faut penser aux intégrales curvilignes, non ? et on écrit :
 ds)
, mais
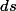
c'est quoi ? quelle différence a -t-il avec
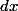
et
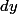
?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2015, 12:53
par barbu23 » 09 Jan 2015, 12:53
Une dernière question :
Lorsqu'on veut intégrer une fonction

sur le cercle unité

, il faut penser aux intégrales curvilignes, non ? et on écrit :
 ds)
, mais
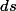
c'est quoi ? quelle différence a -t-il avec
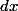
et
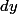
?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
.
.
