Une limite qui me pose probleme

[johndoex3x]

Bonjour,
Je termine mon premier devoir avec un gros blanc au milieu.
Je passe probablement à côté de quelque chose mais toujours est il que je n'arrive pas à prouver cette limite :

pour p fixé inférieur à n et n enter naturel tendant vers l'infini :

1/p! * ( 1- (1-1/n)*(1-2/n)*(1-3/n)*......*(1-(n-p-1)/n)

à priori ça tend vers 0 mais je n'arrive pas à le montrer.
Si vous pouvez m'aider cela me permettrait de finir proprement ce devoir
Merci
Pascal

[MJoe]

Bonjour à tous,

Je commence le calcul de cette expression E :


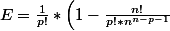Si cela peut aider.

MJoe.

[johndoex3x]

Attention je n'ai pas la formule de Stirling à ma disposition pour l'instant

[MJoe]

Bonjour,

Je ne savais pas.
Est-ce l'expression E que vous avez donnée est l'expression "telle quelle" du sujet ?

MJoe.

[pascal16]

MJoe, c'est pas (n-1)! en haut ?
cette écriture ne nécessite aucune connaissance de limite pour l'instant

j'ai corrigé en (n-1)!

1-1/n = n/n - 1/n = (n-1)/n

[NicoTial]

MJoe, c'est pas (p-1)! en haut ?
cette écriture ne nécessite aucune connaissance de limite pour l'instant

il ne me semble pas non...

[johndoex3x]

1/p! * ( 1- (1-1/n)*(1-2/n)*(1-3/n)*......*(1-(n-(p-1))/n)

désolé une erreur de parenthèses

[pascal16]

Pour la démo, si le problème se rapproche de la formule de Stirling, la démo doit s'en rapprocher aussi.
une démo faite de notion 'simples' :
http://famille-chazal.pagesperso-orange.fr/articles/stirling.pdf
c'est pas jojo

j'ai essayé de calculer ln ( (1-1/n)*(1-2/n)*(1-3/n)*......*(1-(n-(p-1))/n))
je tombe sur une intégrale avec une borne qui dépend de n donc peu utilisable

Calcule un DL en 1/n de (1-1/n)*(1-2/n)*(1-3/n)*......*(1-(n-(p-1))/n)... mais comme pour l'intégrale, la 'borne' dépend de n, n termes d'ordre 1/n donnent du '1' , peu utilisable sans bien faire attention.

Trouver la suite qui va bien ?

[zygomatique]

salut

il est dommage de ne pas connaitre l'espace, les crochets, les accolades en plus des parenthèses pour rendre lisible une formule ...

(1 - 1/n)(1 - 2/n)(1 - 3/n) ... (1 - [n - (p - 1)]/n) = (1 - [n - (n - 1)]/n)(1 - [n - (n - 2)]/n) ... (1 - [n - (p - 1)]/n) = (n - 1)!/[p! n^{n - p + 1} = n!/[p! n^{n - p + 2}]

donc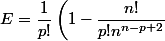

ce me semble-t-il ....

[Kolis]

Bonjour !
Rien de tel pour s'énerver que de s'exciter sur un énoncé faux !
Reconnu par l'auteur sur ce site http://www.les-mathematiques.net/phorum/read.php?4,1504376
Il s'agit de : il y a produit d'un nombre fini de termes.
Et l'auteur avoue :
"et donc effectivement p-1 termes
désolé mais je l'ai tellement retournée dans tous les sens que j'ai fait plusieurs erreurs"
sans revenir corriger son texte ici !

[aymanemaysae]

Bonjour ;

Tout a été dit à propos de ce sujet sur un autre forum .

L'énoncé est comme suit :

avec \ et

On a : donc : produit fini ,

donc :

[MJoe]

Bravo !
Cela semble simple quand on voit la solution !

MJoe.