Transitivité logique

[mehdi-128]

Bonjour,

Soit des assertions quelconques.

On suppose que est vraie et et sont vraies.

Je n'arrive pas à montrer que est vraie.

[chombier]

Tu dois avoir une règle, souvent appelée "Modus Ponens" qui te dit que :

Modus Ponens : Si et sont vraies, alors est vraie

Il faut l'appliquer deux fois.

[mehdi-128]

D'accord merci. Pour le montrer, il faut utiliser les tables de vérité en logique ?

[chombier]

Ça dépends si tu travailles formellement, auquel cas cette règle permet, à partir de deux théorèmes, d'en générer un troisième, ou si tu choisis comme point de vue que chaque assertion un élément de {V ; F} et que le symbole est une loi de composition interne.

Dans le dernier cas, il faut voir comment est définie l'implication. Souvent est défini comme une abréviation de

[mehdi-128]

Dans mon livre est défini comme

Si on a et comment démontrer que est vrai ?

Je rappelle que je n'étudie pas la théorie des ensemble (je ne suis pas à ce niveau), j'étudie un cours de MPSI sur les ensembles.

[chombier]

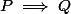
Dans mon livre est défini comme

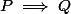
Si on a et comment démontrer que est vrai ?

Je rappelle que je n'étudie pas la théorie des ensemble (je ne suis pas à ce niveau), j'étudie un cours de MPSI sur les ensembles.

J'espère quand même qu'intuitivement ça te parait évident !

Je te conseille de rester sur ton intuition, et d'admettre cette règle : Si P=>Q et P sont vrais, alors Q est vrai.

Sinon il va falloir formaliser beaucoup car c'est difficile de prouver ce qui parait évident.
Tu auras alors principalement deux approches :
- l'axiomatique, dans laquelle la règle que j'ai écrite ci-dessus est souvent énoncée comme un axiome. Mais il y a plusieurs axiomatiques possibles, qui définissent toutes la même structure.
- l'algèbre de Boole. Dans cette approche, on fait souvent des tables de vérité, des tableaux de Karnaugh, il y a aussi une méthode avec des arbres mais je ne retrouve pas son nom.

Tu peux aussi considérer que ce que tu cherches à prouver, c'est que est une tautologie

[mehdi-128]

Ah merci vous avez raison c'est évident !

(NON (P) OU Q ) ET P

Si (NON (P) OU Q ) est vrai et P est vrai alors NON(P) est faux donc forcément Q est vrai.