bonjour,
on note ABC le triangle équilatéral de côté a=AB=AC=BC.
A est est le sommet du haut.
ABC dans le sens trigonométrique positif. (C à droite)
O le centre du cercle circonscrit, de rayon r.
H le milieu de [AC]
on considère le repère polaire
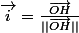
et

l'angle polaire
)
la trigo donne:
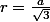
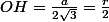
M un point du segment [AC] , M' son image sur le cercle circonscrit
via la demi-droite radiale [OM(
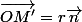
où
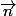
est le vecteur radial normé.
})
} \vec{n})
d'où la transformation
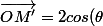 \vec{OM})
valable pour un point M du côté [AC]
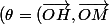))
envoie le côté [AC] sur l'arc AC.
même chose pour le côté [BC]. Pour le côté [AB] la transformation est rentrante, il faut donc refaire les calculs.
finalement, on rassemble les trois transformations en une seule
en discutant selon les valeurs de l'angle polaire.

