(n-1)ln(1-x)+n*x=0

[zobobo]

Bonjour

j'ai montré l'équation (n-1)ln(1-x)+n*x=0 admet une unique solution x_n ds ]0;1[, que x_n tend vers 0 si n tend vers l'infini.
Je dois trouver à présent un équivalent de x_n, ms j'y arrive pas :mur:

Merci de votre aide

[mathelot]

bjr,

on peut remplacer x par car elle est solution.

est aussi un o(1).

Il suffit de faire un DL de ,
avec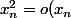


PS: "petit o, grand O"=notation de Landau.

(se lit petit oh, petit eau)

[zobobo]

tu peux détailler stp, je vois pas :help:

[mathelot]

qu'est-ce que tu ne vois pas ? est petit, on fait un DL.

[zobobo]

avec ln(1-x_n) = -x_n+o(x_n), on obtient (1-n)(x_n+o(x_n)) + n*x_n=0
ensuite ??

[mathelot]

on pousse le DL un peu plus loin. :doh:
on essaye de passer à la limite quand
pour voir ce qui se passe.
on simplifie ce qui est simplifiable.

[zobobo]

à l'ordre 2 je vois pas nan plus :triste:
tu peux m'ecrire ta solution stp

[JJa]

Bonjour zobobo,

pourquoi n'écris-tu pas purement et simplement le développement d'ordre 2:
x = a(1/n) + b(1/n²) +...
ou, plus clairement que les trois petits points :
x = a(1/n) + b(1/n²) + O(1/n^3)
et ensuite tu développes en série en remplacant x par l'expression précédente dans :
(1-(1/n))ln(1-x)+x=0
Pour simplifier les écritures, posons :
h=1/n
avec h tendant vers 0.
(1-h)ln(1-x)+x=0
Développement de x au second ordre : x=ah+bh²+O(h^3)
(1-h)(-x-(x²/2)+O(x^3))+x=0
(1-h)(-ah-bh²-((ah)²/2))+ah+bh²=O(h^3)
(-ah-bh²-((ah)²/2))+ah²+ah+bh²=O(h^3)
-((ah)²/2))+ah²=O(h^3)
ah²((-a/2)+1)=O(h^3)
(-a/2)+1=O(h)
donc a=2
Conclusion : x est équivalent à 2h = 2/n
Si les O(h^3) te dérangent, à la place tu n'as qu'à rester avec les trois petits points.
La même méthode, avec un développement en série de plus grand ordre, donnerait le développement asymptotique :
x = (2/n) - (2/3)(1/n²) - (2/9)(1/n^3) - (14/135)(1/n^4) + ...

[mathelot]

pourquoi n'écris-tu pas purement et simplement le développement d'ordre 2:
x = a(1/n) + b(1/n²) +...

on n'est pas sûr qu'un tel développement existe. C'est ce qu'il faut démontrer , en fait.
par ex: tend vers zéro quand n tend vers l'infini mais n'admet pas un DL selon l'échelle ,

[JJa]

Donner une indication pour trouver le résultat n'est pas donner la réponse toute cuite en bonne et due forme.
Il faut bien laisser une certaine initiative pour la présentation de la preuve : cela dépend alors du niveau d'enseignement où le problème est posé.
Sans aller chercher des complications, il pourra toujours commencer en écrivant : "Supposons qu'un développement en série entière de (1/n) existe..."
Ensuite, si le développement est trouvé et prouvé sans apparition de contradiction, ce qui est le cas, que veut-on de plus ?

[zobobo]

Niveau prépa oral de concours.
Mathelot, tu es sur de ta méthode ?
Si oui, tu peux détailler stp :hein:
merci

[Black Jack]

Salut,

ln(1-x) = -x - x²/2 - x³/3 - ... - x^k/k - ... (vrai sur ]-1 ; 1[ et donc a fortiori sur ]0 ; 1[)

(n-1).ln(1-x) + n.x = (n-1).( -x - x²/2 - x³/3 - ... x^k/k - ...) + nx

(n-1).ln(1-x) + n.x = x - (n-1).(x²/2 + x³/3 + ... x^k/k + ...)

(n-1).ln(1-x) + n.x = x - (n-1).(x²/2 + O(x³))

x - (n-1).(x²/2 + O(x³)) = 0

(n-1).x²/2 - x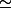 0
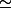(n-1).x/2 - 1 0
x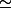 2/(n-1)

Si on veut un poil plus de précision, on prend un terme de plus dans le développement :

x - (n-1).(x²/2 + x³/3)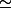 0
(n-1).(x²/2 + x³/3)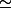 x
(n-1).(x/2 + x²/3)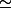 1
2x² + 3x - 6/(n-1)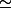 0

x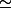 [-3 + V(9 + 48/(n-1))]/4
x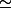 [-3 + V((9(n-1) + 48)/(n-1))]/4
x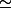 [-3 + V((9n+39)/(n-1))]/4 ... c'est tout de suite moins sympathique à manipuler.

Toutes sottises incluses.