Dl :'(

[Anonyme]

I need help je sens que j'ai de veritables lacunes en Développements limités !
Première situation :
On cherche à étudier la convergence ou pas de la série de terme gnrl :
Un = (n^b)*n!/(a+1)*(a+2)*..........*(a+n)
j'utilise Raabe-Duhand ( soit V(n) = U(n+1)/U(n) )
V(n) = (1+(1/n))^b * (1+(a/n+1))^-1
hop passage au log : V(n) = expo(b*log(1+1/n))*e(-log(1+(a/n+1))
et là on devrait trouver ( ce résultat je ne l'ai pas trouvé perso :( )
V(n) = 1-(a-b)/n + o(1/n²)
et moi je trouve pas ça , et je ne comprends pas comment on peut aboutir à ce résultat notament ce qu'il ya à l'intérieur du landeau ...

Deuxième situation :
x(1+x^2/3 + o(x^2))*(ln(x) + x^2/3 + o(x^2))
on devrait trouver : x*ln(x) + x^3/3*ln(x) + o(x^3*ln(x))
voilà , là aussi je ne comprends pas ce qu'on toruve à l'intérieur du o , svp pouvez me détailler ces deux calculs ( j'ai bcp de lacunes concernant le o , en gros je connais la définition mais dans un calcul pareil je ne sais pas l'appiquer alors essayez de bien expliciter vos calculs )

Je vous remercie infiniment !!

[Anonyme]

raabe-Duhamel plutot :)

[LN1]

Bonjour,

pour la première je pense que c'est plutôt

et cela suffira

technique ln( 1 + h) = h + o(h)

;
En effet qui converge bien vers 0
Or
Donc



Enfin
donc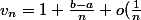

pour la seconde,
en développant tu retrouves les deux termes que tu as écrits , suivis de 7 autres qui sont tous des car si tu les divises par , ils tendent tous vers 0
Je ne vais pas traiter les 7 termes mais seulement deux d'entre eux
est un car qui tend bien vers 0 quand x tend vers 0
est aussi un car qui tend bien vers 0 quand x tend vers 0

Une règle utile (facile à démontrer et rapide à utiliser)
si E = o(a) et que lim (a/b) est finie alors E = o(b)

[Anonyme]

Merci beaucoup d'avoir pris du temps pour me répondre , et merci d'avoir bien détaillé :)
Si tu peux juste , m'expliquer pourquoi o(x^2)/x² tends vers zero ?
pour a/(n+1)* o(a/(n+1)) c égal à zero c ça ?
X*o(x) = 0 tjrs ?

pour la dernière règle , cela veut dire que par exemple lim( a/(n+1) / 1/n ) est fini alors o(a/(n+1)) = o(1/n) ?

Merci de corriger mes erreurs !

[LN1]

pourquoi a pour limite 0 ???? mais c'est la définition même des fonctions négligeables!!!


Au voisinage de a,
f = o(g) ssi il existe une fonction e telle que
*limite en a de e soit nulle
*f = ge

Si g ne s'annule pas dans un voisinage épointé autour de a,
f = o(g) ssi la limite en a de f/g est nulle

C'est la limite du quotient qui doit être nulle, pas celle de produit

Quant à la règle, oui, elle s'applique bien dans le cadre que tu évoques

[Anonyme]

Voilà , je viens de comprendre ya à peine 5mins et tu viens de confirmer ce que je pensais merci bcp ;)
maintenant , une dernière question j'ai remarqué que tu calculais la limite du rapport au voisinage de zero , or par exemple en ce qui concerne le premier dl ( celui de raabe-duhamel ) il s'agissait d'une convergence de série , on ne devrait pas calculer les o au voisinage de l'infini ?

Encore une fois meci , c plus clair dans ma tête à présent :)

[Anonyme]

Enfin c clair les DL sont calculé au voisinage de zero , ici par exemple il ya log(1+a/n) ce qui fait notre affaire , mais ensuite on calcule les rapport avec n-->0 ? c ça qui m'embête merci !

[LN1]

Tu calcules les DL au voisinage de 0 (parfois aussi au voisinage de a), mais tu peux ensuite les composer avec une fonction.
Par exemple, tu utilises le DL de ln(1 + x) au voisinage de zéro,
ln(1 + x) = x + o(x)
Or
donc tu peux remplacer x par 1/n.
Ton égalité devient donc valable au voisinage de + oo.
ln(1 + 1/n) = 1/n + o(1/n)

[Anonyme]

oui certes , mais je voulais parler plutôt de la limite de o(a/n+1)/(1/n) au voisinage de zero , alors que dans l'énoncé on est au voisinage de l'infini ( convergence d'une série ) tu as saisi ma question ?

merci encore une fois :)

[LN1]

Où as-tu vu que je calculais la limite de o(a/n+1)/(1/n) au voisinage de 0 ?

Je regrette en revanche, de n'avoir pas précisé, au voisinage de quoi on se plaçait (pensant que ça allait de soi)

pour n au voisinage de + oo pour le premier calcul

pour x au voisinage de 0 pour le second calcul.

Enfin, je te rappelle que, pour n entier, on ne cherche pas la limite de u_n quand n tend vers 0, car, ou bien n = 0, ou bien n = 1, et n ne peut pas "s'approcher de 0"

[Anonyme]

ok très bien , merci pour toutes ces explications j'y vois bcp plus clair mnt ;)

[Anonyme]

re, encore moi :) ( décidement lol)

alors je pensais avoir compris mais finalement :'( voilà le pb :

sqrt(n^2 + (-1)^n) = n*sqrt(1+(-1)^(n/2)*n^2) = V

1/version yoda :
V = n*(1+(-1)^n/2*n² + o((-1)^n/n²) ( bon là j'ai agis comme un con :))

2/version bouquin :
même expression sauf qu'à l'intérieur du o il ya : o(1/n^4)
et là je ne comprends pas car je ne trouve pas o((-1)^n/n²)/(1/n^4) ---> 0 au voisinage de l"infini !!! ( aussi par quoi , on pourrait remplacer o(...) dans le calcul de la limite moi j'ai mis 1/n^3 par exemple , et donc je trouve pas que ça tends vers 0)

???

merci encore une fois ;)

[LN1]

Bonsoir,

ou bien tu lis mal, ou bien il y a une coquille

DL de au voisinage de 0

ou


pour cela donne

ou

[Anonyme]

lol ah ben dans ce cas peut être bien qu'il s'agit d'une coquille je te copie exactement ce qui est écrit :

sqrt(n²+(-1)^n) = n*sqrt(1+(-1)^n/n²) = n*(1+(-1)^n/2*n² + o(1/n^^4))
alors ?

PS : le bouquin c'est MethodiX Analyse de Xavier Merlin page 114 exemple 20 ( on ne sait jamais )

[Anonyme]

non inscrit c'était moi :)