Bonjour, je suis en première mais j'ai un peu avancé sur le programme des années futures en maths et je me suis posé cette question comment trouver x tel que :
x^x = 4
Sans vraiment le prouver on sait que x=2, mais comment pourrions nous faire pour le démontrer ?
J'ai cherché un peu sur internet et j'ai vu qu'on utilisait la fonction de Lambert W ou un truc comme ça, et ailleurs j'ai vu aussi qu'on obtenait :
log_{x}(4) = x
Mais je ne vois toujours pas comment cela est sensé nous aider. Je pense que le niveau de la question est bien supérieur à celui du lycée et c'est pour ça que je le poste ici. En tout cas si quelqu'un de fort passe par là ça serait cool que l'on m'explique la démarche.
Merci.
X^x=4
3 messages
- Page 1 sur 1
Re: x^x=4
Bonjour,
ln() désigne le logarithme népérien
Le nombre e (e 2,71) est la base des logarithmes.
2,71) est la base des logarithmes.
la solution x=2 est évidente ( car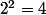 ).
).
Montrons que c'est la seule solution (réelle).
On a
=x^x=e^{x ln(x)})
f est définie et dérivable sur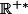
=x^x (ln(x)+1))
pour tout x >0
=0 \Leftrightarrow x=1/e)
Le tableau des variations de f indique que f prend la valeur 4 une seule fois
dans l'intervalle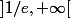 et aucune fois dans l'intervalle ]0;1/e]
et aucune fois dans l'intervalle ]0;1/e]
ln() désigne le logarithme népérien
Le nombre e (e
la solution x=2 est évidente ( car
Montrons que c'est la seule solution (réelle).
On a
f est définie et dérivable sur
pour tout x >0
Le tableau des variations de f indique que f prend la valeur 4 une seule fois
dans l'intervalle
Modifié en dernier par mathelot le 18 Mai 2022, 20:13, modifié 1 fois.
Re: x^x=4
Pour 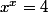 , il y a cette solution évidente.
, il y a cette solution évidente.
Mais si on cherche x tel que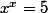 par exemple, alors c'est plus compliqué.
par exemple, alors c'est plus compliqué.
Il y a une racine, quelque part entre 2 et 2.2 ou 2.3 , peu importe pour l'instant.
Les arguments donnés par Mathelot fonctionnent toujours : il n'y a aucune autre racine.
Notre racine, elle vaut combien précisément ? Il n'y a aucune formule toute faite qui va nous donner directement les 4 ou 5 premières décimales de cette racine.
Il n'y a aucune formule du type + b) ou quoi que ce soit de ce genre.
ou quoi que ce soit de ce genre.
La seule méthode , c'est le tâtonnement.
On teste 2.1, on regarde si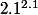 est plus petit ou plus grand que 5. Et selon la réponse, on reteste avec une valeur un peu plus petite ou un peu plus grande.
est plus petit ou plus grand que 5. Et selon la réponse, on reteste avec une valeur un peu plus petite ou un peu plus grande.
Je parle de 'tâtonnement', mais il y a des méthodes efficaces pour tâtonner plus vite que celui qui tâtonnerait sans méthode.
La discipline qui permet d'étudier ces outils de tâtonnement, ça s'appelle le calcul numérique. C'est un terme un peu fourre-tout, puisque c'est aussi comme ça qu'on appelle des calculs qu'on peut faire au collège.
cf : https://fr.wikipedia.org/wiki/Calcul_num%C3%A9rique
Mais si on cherche x tel que
Il y a une racine, quelque part entre 2 et 2.2 ou 2.3 , peu importe pour l'instant.
Les arguments donnés par Mathelot fonctionnent toujours : il n'y a aucune autre racine.
Notre racine, elle vaut combien précisément ? Il n'y a aucune formule toute faite qui va nous donner directement les 4 ou 5 premières décimales de cette racine.
Il n'y a aucune formule du type
La seule méthode , c'est le tâtonnement.
On teste 2.1, on regarde si
Je parle de 'tâtonnement', mais il y a des méthodes efficaces pour tâtonner plus vite que celui qui tâtonnerait sans méthode.
La discipline qui permet d'étudier ces outils de tâtonnement, ça s'appelle le calcul numérique. C'est un terme un peu fourre-tout, puisque c'est aussi comme ça qu'on appelle des calculs qu'on peut faire au collège.
cf : https://fr.wikipedia.org/wiki/Calcul_num%C3%A9rique
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
