V = (Im(f*)df/dx)/|f|²

par **davlabulle** » 30 Nov 2006, 05:22

Bonjour

quelqu'un connait il ou a entendu parler de cette formule ?

v = (Im(f*)df/dx)/|f|²

Je ne sais pas a quoi elle correspond ni dans quel contexte elle se place

Merci par avance

par **jlv** » 18 Jan 2007, 20:45

Moi aussi je cherche le sens de cette formule. Tenons-nous au courant ! a bientôt
JLV

par **fahr451** » 18 Jan 2007, 20:49

Im pour imaginaire j 'imagine , mais * ou conjugué?

c'est un peu vague désolé .

par **mathelot** » 19 Jan 2007, 06:14

bonjour,
en m'aidant des remarques précédentes,

il ne reste plus qu'à poser:

d'où:

ça se simplifie:

en prenant la partie imaginaire:

par **Firenigma** » 20 Fév 2007, 10:29

En francais sa veut dire quoi se calcul ?

La formule v = (Im(f*)df/dx)/|f|² démontre quoi au juste, que l'imaginaire est infini ?

par **mathelot** » 21 Fév 2007, 07:37

bonjour,

la fonction v que vous indiquez est la partie imaginaire de la dérivée
par rapport à la variable

du logarithme d'une fonction f complexe.
Concernant les fonctions complexes, la dérivée par rapport à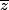

est particulièrement intéressante car cette dérivée est nulle si et seulement si f est holomorphe.

par **Firenigma** » 25 Fév 2007, 01:44

Merci pour votre réponse,mais elle est encore beaucoup trop mathématique.
Je crois m'avoir mal exprimé j'aurrais du demander de me vulgariser cette formule.

V = (Im(f*)df/dx)/|f|²

v = (Im(f*)df/dx)/|f|²

Qui est en ligne