Bonjour,
J'aurais deux questions sur lesquelles je sèche particulièrement:
- si on suppose qu'un couple A² d'anneaux possède un PGCD, comment peut-on montrer que des éléments a et b de l'anneau A possèdent un PPCM ?
- comment peut-on montrer qu'un anneau A est bézoutien car il vérifie le théorème de Bezout ET parce que tout couple de A² possède un PGCD ?
Merci par avance, cela fait partie d'une série de questions sur l'arithmétique et les anneaux, je bloque sur ces questions assez sévèrement et je n'ai aucune idée ( enfin si, mais c'est trop vague ) donc inutile d'essayer de "me sortir les vers du nez" :ptdr:
Quelques pistes ?
A bientot :we:
2 messages
- Page 1 sur 1
Salut : :happy3:
Supposons que :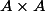 possède un
possède un 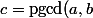) pour tout
pour tout  \in A \times A) , et on note :
, et on note : ) .
.
Donc, il existe un plus petit idéal) tel que :
tel que : 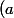 \subset (c)) et
et  \subset (c)) et
et  = (a) + (b)) . Il suffit de prendre :
. Il suffit de prendre : 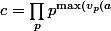,v_p(b)}) avec :
avec :  un nombre premier. Cela ne peut avoir lieu que si
un nombre premier. Cela ne peut avoir lieu que si  est factoriel, pour avoir la permission d'écrire :
est factoriel, pour avoir la permission d'écrire : 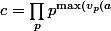,v_p(b)}) .
.
Si est factoriel.
est factoriel.
Il existe un plus grand idéal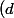) avec
avec 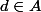 et
et 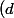 \subset (a)) et
et 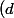 \subset (b)) et
et 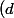 = (a) \bigcap (b)) .
.
Il suffit de prendre :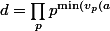,v_p(b)}) .
.
Dans le cas où est général ( i.e : non nécessairement factoriel ) attend un peu, je vais y réfléchir. :happy3:
est général ( i.e : non nécessairement factoriel ) attend un peu, je vais y réfléchir. :happy3:
Cordialement. :happy3:
Edit : Pour le cas non factoriel, tu montres qu'il existe un plus petit idéal principal
non factoriel, tu montres qu'il existe un plus petit idéal principal  tel que
tel que 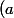 \subset I) et
et  \subset I) et
et })) . Le
. Le ) est dans ce cas là :
est dans ce cas là :
 = \dfrac{ab}{\mathrm{pgcd} (a,b)})
Supposons que :
Donc, il existe un plus petit idéal
Si
Il existe un plus grand idéal
Il suffit de prendre :
Dans le cas où
Cordialement. :happy3:
Edit : Pour le cas
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
