Un+1 = un + ln(un)

[tist]

Bonjour,

est-ce qu'à tout hasard quelqu'un connaît un exo d'étude d'une suite un+1 = un + ln(un) ?
(suite à laquelle je m'intéresse un peu par hasard disons)
Pas de problème pour montrer les résultats classiques (si u0<1 , la suite n'est plus définie à partir d'un certain rang, si u0=1 la suite est constante, si u0>1 la suite diverge vers + infini) mais en fait je cherche un équivalent de (un) dans ce dernier cas.
J'ai essayé quelques méthodes classiques (théorème de Cesaro à ln(un+1) - ln(un) par exemple) mais sans succès. Je trouve juste que ln(un) est négligeable devant n
Je préviens je ne sais pas si c'est simple, je demande juste au cas où vous avez déjà traité cet exo!
Merci!

[arnaud32]

qu'et ce que tu penses de x+ln(x)= x(1+ln(x)/x)
quelle est la limite de x -> ln(x)/x en +oo
quelle est la definitiopn d'un equivalent?

[adrien69]

Salut, j'ai une astuce.
Ça marche mais c'est assez WTF dans l'idée...

[adrien69]

Une idée comme ça en passant :
Essaie d'étudier la suite
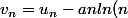(en fait plutôt )
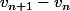En choisissant a posteriori a pour trouver un truc bien.
Je ne suis pas arrivé au bout parce que je viens de penser à introduire a comme un paramètre et que je n'ai pas trop de temps, mais ça m'a l'air d'aboutir grâce à une comparaison série-intégrale.