P'tit soucis avec la continuité de la fonction gamma

[senpai.nl]

Salut,

Voilà pour être vif, j'arrive pas à comprendre le corrigé de la premiere question de cet exercice :http://www.math.u-bordeaux1.fr/~frgaunar/fonctiongamma.pdf
(desolé je n'ai aucune idée sur comment inserer les caracteres sur ce post )

Sinon, pour vous expliquer mon probleme , bah dans la premiere question , on demande de montrer que gamma est definie sur ]0;+00[, normalement pour montrer qu'une integrale est definie ,il suffit de montrer que la fonction à l'interieur de l'integrale est continue. Dans le cas de la fonction gamma , on a exp(-t)t^(x-1) est continue sur R pour tout x>1 (car elle est le produit de 2 fonctions continues sur R). Dans le corrigé on detaille les 2 cas du voisinage de 0 et celui de +00 , quelqu'un peut m'expliquer pourquoi? :mur:

En attendant vos reponses , je m'excuse pour ce post trés trés mal presenté ( c'est ma premiere fois , je ne suis pas habitué à utiliser des forums en math )

[newman]

Salut,

Voilà pour être vif, j'arrive pas à comprendre le corrigé de la premiere question de cet exercice :http://www.math.u-bordeaux1.fr/~frgaunar/fonctiongamma.pdf
(desolé je n'ai aucune idée sur comment inserer les caracteres sur ce post )

Sinon, pour vous expliquer mon probleme , bah dans la premiere question , on demande de montrer que gamma est definie sur ]0;+00[, normalement pour montrer qu'une integrale est definie ,il suffit de montrer que la fonction à l'interieur de l'integrale est continue. Dans le cas de la fonction gamma , on a exp(-t)t^(x-1) est continue sur R pour tout x>1 (car elle est le produit de 2 fonctions continues sur R). Dans le corrigé on detaille les 2 cas du voisinage de 0 et celui de +00 , quelqu'un peut m'expliquer pourquoi? :mur:

En attendant vos reponses , je m'excuse pour ce post trés trés mal presenté ( c'est ma premiere fois , je ne suis pas habitué à utiliser des forums en math )

Attention, tu ne travailles pas sur un segment!! Il faut donc vérifier que la fonction est continue (en fait continue par morceaux ça suffit)...mais aussi qu'elle est intégrable(le plus important)...

J'espère que ce rappel te fera comprendre tout l'intérêt de la question 1

[senpai.nl]

Attention, tu ne travailles pas sur un segment!! Il faut donc aussi vérifier que la fonction est continue (en fait continue par morceaux ça suffit)...mais aussi qu'elle est intégrable(le plus important)...

J'espère que ce rappel te fera comprendre tout l'intérêt de la question 1

en effet, je viens de verrifier mon cours , continue=> integrable dans le cas d'un segment (merci pour le rappel) mais sinon en gros ,a part la continuité, comment montrer qu'une fonction est integrable ? Sinon une question encore plus bête , que veux dire une integrale convergente ?

Merci encore et desole pour le mal que je vous donne

[alm]

Bonsoir :
Dans tout ce qui suit i est un intervalle de \mathbb R et f une fonction continue par morceaux sur i à valeurs dans \mathbb R ou \mathbb C.

Revenons à la question :
Trés bonne question.
En effet c'est vrai , il y a une différence énorme entre:
-integrale convergente
- fonction integrable.

Avant de détailler on dit tout de suite :
Si est integrable sur alors l'integrale est convergente.

Ensuite on rappelle :
On dit que est convergente si une primitive de sur admet des limites finies aux bornes de dans ce cas si on appelle et 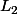ces limites respectivement pour la borne inf et la borne sup de alors est le résultat ne dépends pas de la primitive choise (différent d'une cosntante additive)


On dit que est integrable sur si est convergente

Si f est integrable sur alors est convergente et :

Remarques:
1) on dit aussi abolument convergente au lieu de integrable.
2) On dit aussi sommable pour integrable
3) si est convergente sans que f soit integrable sur , on dit que l'integrale est semi-convergente.
Exemple et

[newman]

en effet, je viens de verrifier mon cours , continue=> integrable dans le cas d'un segment (merci pour le rappel) mais sinon en gros ,a part la continuité, comment montrer qu'une fonction est integrable ? Sinon une question encore plus bête , que veux dire une integrale convergente ?

Merci encore et desole pour le mal que je vous donne

Pour montrer qu'une fonction est intégrable,on invoque le théorème de comparaison des fonctions positives...pour l'utiliser on compare la fonction à intégrer avec une "fonction de riemann" du style "1/t²"...Bref c'est tout un chapitre à assimiler ca s'explique pas en 2 lignes

Je pense donc qu'il est un peu ambitieux pour le moment d'attaquer l'étude de la fonction Gamma sans avoir fait au préalable une batterie d'exos pratiques simples sur l'intégrabilité d'une fonction et bien avoir compris son cours

l'intégrale est convergente si tu obtiens un résultat fini en intégrant la fonction sur tout l'intervalle(souvent non borné...comme [0:+infini[ )

[senpai.nl]

En lisant vos deux reponses , ca devient de plus en plus clair. Je pense,comme vous l'avez proposé, que je dois m'exercer sur des integrales plus simples. Mon probleme c'est que j'ai mal geré ma premiere année en sup, chose qui m'a payé beaucoups de lacunes dont je payes le prix aujourdhui en preparant mes concours...
Bref, merci infiniment à vous deux pour votre patience. A bientot.

[newman]

En lisant vos deux reponses , ca devient de plus en plus clair. Je pense,comme vous l'avez proposé, que je dois m'exercer sur des integrales plus simples. Mon probleme c'est que j'ai mal geré ma premiere année en sup, chose qui m'a payé beaucoups de lacunes dont je payes le prix aujourdhui en preparant mes concours...
Bref, merci infiniment à vous deux pour votre patience. A bientot.

euhh les concours c'est fini là non..(à part la fin de e3a demain..)

[alm]

En lisant vos deux reponses , ca devient de plus en plus clair. Je pense,comme vous l'avez proposé, que je dois m'exercer sur des integrales plus simples. Mon probleme c'est que j'ai mal geré ma premiere année en sup, chose qui m'a payé beaucoups de lacunes dont je payes le prix aujourdhui en preparant mes concours...
Bref, merci infiniment à vous deux pour votre patience. A bientot.

Ne te fait pas trop de reproche: c'est le cas pour beaucoup d'élèves en spé : ils n'avaient pas le temps de travailler un grand nombre d'exos
pour toi n'hésite pas de poser toutes tes questions là dessus , on fera de notre mieux pour t'aider à bien comprendre.

Pour Gamme ce n'est pas délicat pour ce qui est de son ensemble de définition.
Quand tu sera prét on reprendera tout ça avec soin.

[newman]

Ne te fait pas trop de reproche: c'est le cas pour beaucoup d'élèves en spé : ils n'avaient pas le temps de travailler un grand nombre d'exos
pour toi n'hésite pas de poser toutes tes questions là dessus , on fera de notre mieux pour t'aider à bien comprendre.

Pour Gamme ce n'est pas délicat pour ce qui est de son ensemble de définition.
Quand tu sera prét on reprendera tout ça avec soin.

Merci Mohamed pour l'aide que tu apportes sur le forum

[senpai.nl]

euhh les concours c'est fini là non..(à part la fin de e3a demain..)

je suis marocain , on a encore du temps :zen:

[alm]

Merci Mohamed pour l'aide que tu apportes sur le forum

Je t'en prie newman ! merci à toi aussi.

[alm]

je suis marocain , on a encore du temps :zen:

Moi je n'ai plus de temps que d'ici fin juillet.
Il suffit d'être sur le forum et d'aimer comprendre les maths :marteau: la nationalité .

[senpai.nl]

De retour , une question qui n'a rien à voir avec cet exercice. J'ai remarqué que généralement pour montrer qu'une fonction est intégrable on utilise soit la comparaison soit l’équivalence avec d'autre fonction.. Et là on dit directement (dans les corrigés) que ces fonctions sont intégrables sans démonstration alors qu'en générale elle ne sont pas mieux que celle de départ (exemple devant les mains : intégrale de t.exp(-t²) entre 0 et +00) (désolé pour l’écriture je fais de mon mieux :cry: )
Est-ce qu'il y a des intégrales 'remarquables' dont on a le droit de mentionner l’intégrabilité directement? je connais déjà la fonction 1/t^a où a>1, mais y en a-t-il d'autre?

[alm]

intégrale de t.exp(-t²) entre 0 et +00) (désolé pour l’écriture je fais de mon mieux )
Est-ce qu'il y a des intégrales 'remarquables' dont on a le droit de mentionner l’intégrabilité directement? je connais déjà la fonction 1/t^a où a>1, mais y en a-t-il d'autre?

Oui, les intégrales remarquables que donne le cours comme:
celle de Riemann (celle que tu as cité)
(converge ssi si est complexe non réel elle converge si et elle converge absolument alors )
qui est convergente (absolument même) il suffit d'utiliser une primitive


Pour l'exemple de la technique utilisée c'est de la comparer avec avec a réel judicieusement choisi
Ici convient on a ce qui veut dire qu'au voisinage de on a et les théorèmes parlent là dessus ...

[MyLifeIsMathematic]

Salut c'est toujours moi (senpai.nl) j'ai eu quelques problemes avec mon ancien compte donc j'ai crée un nouveau..
Bref pour revenir au sujet , j'ai fait quelques exercices simples et c'est encore plus clair qu'au debut mis à part quelques points encore pas compris à propos de l'exercice de la fonction gamma.
Pour commencer, je pense qu'on est tous d'accord que pour tout x de ]0,+00[ la fonction t--->exp(-t).t^(x-1) est continue sur tout R n'est-ce pas? Alors pourquoi doit-on verrifier le voisinage de 0? Pourquoi ne pas dire que cette fonction est continue sur tout R en particulier sur [0,1] qui est un compact donc integrable au sens de Riemann sur le meme intervalle?Je suis sur que je me trompe mais je ne sais pas où.
Sinon deuxieme question, quand on utilise un procedé de comparaison (par exemple l'equivalence) au voisinage de l'infini, la continuité est necessaire? je sais que la positivité l'est mais qu'en est-il de la continuité? Sur des livres on ne la mentionne pas mais sur mon cours elle l'est ?
Voilà en attendant vos reponses, je vous souhaite une bonne soirée :lol3: