Bonjour,
j'ai un souci avec cet exercice:
L'énoncé de ce théorème est le suivant:
Soient

,

deux espaces affines réels de même dimension

(
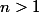
) et

une application bijective de

dans

. Alors

est une application affine si et seulement si elle envoie trois points alignés sur trois points alignés.
On part de l'hypothèse que

envoie trois points alignés sur trois points alignés.
a) Montrer que si

est un sous-espace affine de

, alors
)
est un sous-espace affine de

.
b) Soit

un hyperplan de

. Montrer que la dimension de
)
est strictement inférieure à

.
En déduire que les images par

des points d'une base affine de

forment une base affine de

, puis que les images de

points (
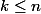
) affinement indépendants sont affinements indépendants.
c) En déduire que l'image d'une droite est une droite, l'image d'un plan est un plan, puis que les images de deux droites parallèles forment deux droites parallèles.
d) Montrer que si
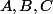
et

sont des points de

non colinéaires avec
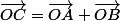
alors les images

des points
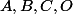
par

vérifient:

.
Soient

et

deux points distincts de

. Pour tout réel

, on considère le point

tel que

. Remarquer qu'il existe un unique réel
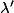
tel que

.
On peut donc définir une application de

dans

:
:=\lambda')
.
e) Soient

et

deux points de

tels que

et

. En utilisant un point

auxiliaire hors de la droite
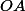
et des parallèles construire le point

tel que
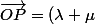\vec{OA})
.
Par une méthode analogue, construire le point

tel que
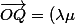\vec{OA})
.
f) Déduire des constructions précédentes que

est un endomorphisme du corps de

, et donc que

est l'application identité.
g) Montrer que

est affine.
h) On vient de montrer un sens du théorème. Que pensez-vous de la réciproque?
i) Montrer que les hypothèses
( )
),
(f bijective) et (le corps de base est

) sont nécessaires.
Déjà pour la a), je ne vois pas comment faire :hein:
Merci pour votre aide.
