Théorème fondamental de l'arithmétique
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 26 Juin 2010, 08:59
par jeje56 » 26 Juin 2010, 08:59
Bonjour,
Je propose cette démonstration de l'unicité de la décomposition en produits de facteurs premiers :
Soit H_n la propriété :
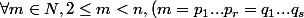\Rightarrow (r=s,p_i=q_i))
où :

et

H_3 est vraie :

Supposons
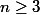
et H_n vraie ;
p_1 divise q_1...q_s donc il existe j tel que p_1 divise q_j
Or q_j étant premier, p_1=q_j
Donc,

(q_1 plus petit des q_j)
De même, on montre

D'où : p_1=q_1
En simplifiant par p_1, l'hypothèse de récurrence assure que p_2=q_2,...,p_r=q_s et que r-1=s-1 puisque n/p_1 strictement inférieur à n
D'où H_(n+1) est vraie
Voilà

-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 28 Juin 2010, 13:52
par Doraki » 28 Juin 2010, 13:52
jeje56 a écrit:En simplifiant par p_1, l'hypothèse de récurrence assure que p_2=q_2,...,p_r=q_s et que r-1=s-1 puisque n/p_1 strictement inférieur à n
D'où H_(n+1) est vraie
non, l'hypothèse de récurrence ne s'applique pas quand n/p1 = 1.
-
jeje56
- Membre Irrationnel
- Messages: 1187
- Enregistré le: 16 Jan 2007, 20:10
-
 par jeje56 » 28 Juin 2010, 14:18
par jeje56 » 28 Juin 2010, 14:18
A première vue, c'est vrai... Où faudrait-il distinguer ce cas ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 84 invités
