Théorème fondamental de l'analyse non vérifié

[zaidoun]

Bonjour,

Je cherche un exemple qui vérifie, pour une fonction f dérivable:

[Pseuda]

Bonsoir,

??? C'est le théorème fondamental de l'analyse. On va donc avoir du mal à trouver un contre-exemple.

Peux-tu préciser pour des intervenants plus qualifiés que moi sur ce genre de questions : f est une fonction réelle, a et b sont bien dans ?

[Robot]

Il y a des fonctions qui ont des dérivées non intégrables. Mais alors l'écriture n'a pas de sens.

[zaidoun]

f est une fonction réelle , a et b sont réels. En fait ce théorème est vrai pour toute fonction f de classe C^1

et il peut être faux si on suppose que f est uniquement dérivable, mais je trouve pas un contre-exemple.

[zaidoun]

@ Robot: non intégrable au sens de Riemann???

l'intégrale de f' n'a pas un sens veut dire que l'intégrale de f' diverge, c'est ça??

Existe-t-ils des fonctions dérivables dont les dérivées sont intégrables mais qui ne vérifient pas

???????????

[Robot]

A partir du moment où f' est intégrable, on aura l'égalité.
f' non intégrable veut dire que f' n'est pas intégrable. Tu sais ce que veut dire une fonction intégrable au sens de Riemann, n'est-ce pas ?

[zaidoun]

pouvez vous me donner des exemples (avec f est uniquement dérivable): si f' est intégrable, alors l'égalité est vérifiée.

et aussi des exemples qui vérifient pas l'égalité càd des exemples où f' non intégrable.

Merci bien.

[Robot]

pouvez vous me donner des exemples (avec f est uniquement dérivable): si f' est intégrable, alors l'égalité est vérifiée.

????? Tu prends n'importe quelle fonction dont la dérivée est intégrable (par exemple continue).

des exemples où f' non intégrable.

Il y a l'exemple souvent donné de à dérivée non bornée et donc non intégrable Riemann, mais c'est un peu triché. Il y a des exemples de fonctions à dérivée bornée et non intégrables Riemann, mais ils sont difficiles à construire et je ne pourrais pas les donner comme ça. Une référence que j'ai retrouvée :
Problème 2.4.31 de W.J. Kaczor, M.T. Nowak, Problems in Mathematical Analysis III, Integration, AMS, 2003
Peut-être aussi dans le livre de Hauchecorne.

Tout ça dépend de la théorie de l'intégration utilisée.

[Kolis]

Bonsoir !
Voici un exemple (très raccourci) où une fonction dérivée bornée n'est pas Riemann-intégrable. Ne disposant pas des sources indiquées par Robot il n'est pas impossible que cet exemple soit justement le sien !

Soit une partie dense dénombrable de une bijection de sur et .
On peut montrer que la série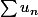 définit sur une fonction de dérivée infinie pour 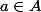et pour tel que est divergente. Sinon est dérivable et la dérivée minorée par .

Alors la fonction réciproque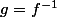 a une dérivée bornée, positive, de dérivée nulle sur un ensemble contenant (correction : contenant f(A)). Si était intégrable, comme elle est nulle sur un ensemble dense, l'intégrale serait nulle et égale à .

[zaidoun]

Merci beaucoup pour vos réponses