Bonjour à tous, voila j'ai un problème de mathématiques financières, j'ai beau m'y pencher dessus, je ne trouve pas la démarche. Donc si vous pouviez m'éclairer, je vous en serai très reconnaissant. Le problème est le suivant:
Une personne emprunte une somme S, le 1er janvier 2008, à un taux d'interêt annuel t. Elle remboursera par annuités constantes notées A et versées chaque 1er janvier, pendant p années, à partir du 1er janvier 2009. On note Cn le capital restant dû le 1er janvier de l'année 2008+n (après le calcul des intérêts et le versement de la nième annuité A), n étant une entier inférieur ou égal à p.
1)a) Calculer C1 et C2. établir une relation entre Cn et Cn+1. Préciser la nature de la suite {Cn}.
Démontrer que Cn=(1+t)^n [S- (A/t)] + (A/t)
Indiquez la valeur numérique de Cp.Montrer que:
[INDENT] t[/INDENT]
A= S -------------
[INDENT]1-(1+t)^-p[/INDENT]
En déduire que
[INDENT] (1+t)^p -(1+t)^n[/INDENT]
Cn= S[ -------------------]
[INDENT](1+t)^p - 1[/INDENT]
Voila, il y a une suite, mais je pense que la c'est déja beaucoup.
En espérant que vous pourrez m'aider (dsl pour les fractions, c'est pas très beau...)
Merci
TECHNIQUES QUANTITATIVES, intérêts composés
4 messages
- Page 1 sur 1
Kapital restant dû
aloha,
il s'agit d'un plan d'amortissement très classique. Le principe:
On rembourse A chaque année.
Dans ce remboursement A, il y a une partie d'intérets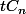 .
.
La partie de capital remboursé est donc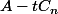
le capital restant est donc:
)
le capital restant est donc une suite arithmético-géométrique.
soit L son point fixe, vérifiant l'équation au point fixe:
L -A)
La suite de terme général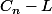 est donc géométrique.
est donc géométrique.
A la fin de l'échéancier, on écrit que le capital à rembourser
est nul, soit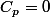 ou
ou 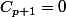 ,
,
je ne sais pas trop, ce qui permet :
i) de calculer p avec un log
ii) d'utiliser l'égalité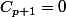 pour la suite.
pour la suite.
n'hésite pas à poser des questions...........
il s'agit d'un plan d'amortissement très classique. Le principe:
On rembourse A chaque année.
Dans ce remboursement A, il y a une partie d'intérets
La partie de capital remboursé est donc
le capital restant est donc:
le capital restant est donc une suite arithmético-géométrique.
soit L son point fixe, vérifiant l'équation au point fixe:
La suite de terme général
A la fin de l'échéancier, on écrit que le capital à rembourser
est nul, soit
je ne sais pas trop, ce qui permet :
i) de calculer p avec un log
ii) d'utiliser l'égalité
n'hésite pas à poser des questions...........
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
