Techniques de diagonalisation

[nix386]

bonjour je suis entrain de préparer le capes l examen est sous la forme d un qcm de 80 question en une heure donc en moyenne t as 45 secondes par question donc pas le temps de faire des calcules minutieux
s il vous plait j ai besoin de quelques technique de diagonalisable
Énoncé:

Mes réponses
pour la première question j ai utilisé la règle SARUS j ai trouvé la réponse D
les autres matrices sont de rang 2 donc 0 est une valeurs propre d ordre 1 = 3-2 qlq1 peut démontrer ce résultat pourquoi lorsque le rang de la matrice est inférieur a sa dimension alors 0 est une valeur propres
qlq1 peut me donner comment répondre a ces question rapidement ou me donner des technique a utilisé dans les cas comme ça
merci

[Arnaud-29-31]

Salut,

Q23 : Ca marche avec Sarus mais c'est plus immédiat avec un développement suivant la 1ere ligne.

Q24 : de manière immédiate grâce à un développement suivant la dernière colonne. Et donc 0 est bien vp

Pour 25 et 26 pareil, le polynôme caractéristique s'obtient par développement sur la dernière ligne et on a 0 vp simple 2 vp double. La matrice est bien de rang 2 et elle est diagonalisable.

[nix386]

Salut,

Q23 : Ca marche avec Sarus mais c'est plus immédiat avec un développement suivant la 1ere ligne.

Q24 : de manière immédiate grâce à un développement suivant la dernière colonne. Et donc 0 est bien vp

Pour 25 et 26 pareil, le polynôme caractéristique s'obtient par développement sur la dernière ligne et on a 0 vp simple 2 vp double. La matrice est bien de rang 2 et elle est diagonalisable.

tu m as dit que la matrice est diagonalisable comment t as su t as chercher la dim ker(A-2I) ??
donc son polynôme minimal est X(X-2)² c est ça ?

[Arnaud-29-31]

Oui ... ca se voit de suite car résoudre AX = 2.X revient à résoudre dont l'ensemble solution est clairement de dimension 2.

Pour le polynôme minimal, on cherche un polynôme de plus bas degré possible, unitaire, diviseur du polynôme caractéristique et annulant A.

[nix386]

Oui ... ca se voit de suite car résoudre AX = 2.X revient à résoudre dont l'ensemble solution est clairement de dimension 2.

Pour le polynôme minimal, on cherche un polynôme de plus bas degré possible, unitaire, diviseur du polynôme caractéristique et annulant A.

stp une dernière demande resoud moi (A-2I)X=0 et donne moi les deux vecteurs propres stp

[Arnaud-29-31]

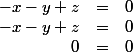
Bein AX = 2X ca revient à résoudre Donc -x-y+z = 0 : On peut prendre (1,0,1) et (1,-1,0) comme vecteurs propres par exemple.

[nix386]

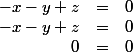
Bein AX = 2X ca revient à résoudre Donc -x-y+z = 0 : On peut prendre (1,0,1) et (1,-1,0) comme vecteurs propres par exemple.

comment on voit exactement a partire du syeteme que dim (ker(a-2I))=2 est ce que on peut dire que puisque rang(A-2I)=1 donc dim (ker(A-2I))=3-1=2 ?

[Arnaud-29-31]

Oui on peut dire ca.