Tan(cotan(x))=cotan(tan(x))

[dilzydils]

Bonjour

Je dois resoudre cette equation, apres qq tentatives, je n'aboutis à rien de concret.

Merci de vore aide

[yos]

Le premier membre est égal à x (quel que soit le réel x).
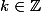
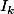
Le second membre est défini sur la réunion des intervalles où . Dans l'un de ces intervalles , le second membre est égal à .
L'égalité des deux membres est réalisée ssi k=0.
L'ensemble de solution est donc .

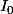
[Nightmare]

Bonjour Yos

tu ne confonds pas cotan et Arctan ?

[dilzydils]

??
cotan(x)=1/tan(x). C'est pas arctan

[yos]

Bonjour Yos

tu ne confonds pas cotan et Arctan ?

Ah si! J'ai lu ce que j'avais envie de voir en fait.

[yos]

on a cos ((t²+1)/t)= 0

(t²+1)/t = +-Pi/2 (on a déjà t0 [Pi] plus haut)

donc t²+-t*Pi/2 + 1 = 0
Delta < 0 donc pas de solutions.


A vérifier j'ai fait ça d'un trait. Y a surement des erreurs quelque part.

Tu dois pouvoir écrire (t²+1)/t = +-Pi/2 +k pi et pour k différent de 0 et -1, l'équation du second degré a des solutions.

[yos]

Je me trompe ?

Je pense que Dilzydils pourra en juger.