Suite Fibonacci et récurrence

[chan79]

Bonjour ,
J'ai du mal avec la récurrence surtout pour l’hérédité
L'exercice est
On pose F0=0 F1=1 puis pour tout n>=2 on pose Fn=Fn-1+Fn-2
On a A:=(1+ 5)/2 et B:=(1-;)5)/2
Je dois montrer par récurrence que pour tout entier n>=2 on a Fn=(a^n-b^n)/;)5

L'initialisation c'est bon
Mais pour l’hérédité je n'arrive pas
on a Fn=(a^n-b^n)/;)5 on cherche à montrer que Fn+1=(a^n+1-b^n+1)/;)5
On a Fn+1=Fn+Fn-1 d'après Fn=Fn-1+Fn-2
D'après l’hypothèse de récurrence on a Fn mais après pour Fn-1 je dois utiliser Fn=Fn-1+Fn-2 ou plutôt Fn=(a^n-b^n)/;)5 ?
Merci pour votre aide

Salut
tu dois donc démontrer que
+=
tu peux enlever les dénominateurs
Transforme ce qui est à gauche pour obtenir ce qui est à droite
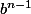
Mets et en facteurs et bien-sûr, remplace ensuite a et b par leurs valeurs

[Kikoo <3 Bieber]

encore une question désolée
Maintenant je dois montrer que Fn>a^(n-2)
Je voulais savoir je pars de la question précédente c'est à dire de Fn=(a^n-b^n)/ racine carrée de 5 ?
Pour montrer que Fn+1>a^(n-1)
Merci par avance

Salut,
Oui tu fais un raisonnement par récurrence.