Somme finie
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
perlman
- Membre Naturel
- Messages: 26
- Enregistré le: 05 Juil 2009, 12:19
-
 par perlman » 05 Juil 2009, 12:21
par perlman » 05 Juil 2009, 12:21
bonjour,
J'aurai besoin de calculer la somme suivante: sigma(k*k!) k va de 0 jusqu'à n.
Merci
 par busard_des_roseaux » 05 Juil 2009, 14:17
par busard_des_roseaux » 05 Juil 2009, 14:17
bonjour,
en écrivant k=(k+1)-1,la somme devient téléscopique
-
perlman
- Membre Naturel
- Messages: 26
- Enregistré le: 05 Juil 2009, 12:19
-
 par perlman » 05 Juil 2009, 15:01
par perlman » 05 Juil 2009, 15:01
mille merci

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 06 Juil 2009, 17:06
par Ericovitchi » 06 Juil 2009, 17:06
télescopique, télescopique, ... allons jusqu'au bout pour voir, c'est intéressant mais je ne suis pas sûr d'avoir vraiment saisi :
J'ai déduis de l'astuce de busard que Sn s'écrivait
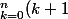 ! - \bigsum_{k=0}^{n} k ! = -1 + \bigsum_{k=0}^{n+1} k ! - \bigsum_{k=0}^{n} k ! = (n+1)!-1)
C'est juste ça ?
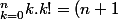!-1)
c'est sympa comme formule :we:
Du coup vous avez vu, ça permet aussi de calculer une formule pour

-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 06 Juil 2009, 22:03
par Luc » 06 Juil 2009, 22:03
Bonjour,
Ericovitchi a écrit:Du coup vous avez vu, ça permet aussi de calculer une formule pour

Quelle formule obtient-on?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 07 Juil 2009, 16:54
par Ericovitchi » 07 Juil 2009, 16:54
non je me suis trompé, ça n'est pas si simple finalement de trouver une formule pour

Si quelqu'un voit une astuce ?
-
Luc
- Membre Irrationnel
- Messages: 1806
- Enregistré le: 28 Jan 2006, 12:47
-
 par Luc » 07 Juil 2009, 18:33
par Luc » 07 Juil 2009, 18:33
Ok je suis à la fois rassuré et déçu :zen:
Je ne pense pas qu'une telle formule existe, mais sait-on jamais.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
