Serie avec paramètre

[cedric125]

bonsoir besoin d'aide sur cet exos:
discuter suivant les valeurs du paramètre reel a,x la nature de la serie:





nous en avons parlons brièvement sur cette partie en cour...est ce que c'est possible d’utilisé les théorème de comparaison,d’équivalence ou d'Alembert?

[tournesol]

tu peux utiliser tout théorème qui renseigne sur la nature de ces séries.

[Tuvasbien]

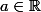
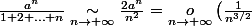J'imagine que et . Pour le 1), il y a plusieurs cas à traiter : si alors la série diverge grossièrement, si , la série est alternée et tu peux utiliser le critère spécial des séries alternés, si alors bien sûr la série converge et si alors comme et qu'il s'agit de séries à termes positifs, la série converge. Pour le reste c'est plus simple, pour la 2) est-ce que le terme général tend vers ? 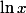Pour la 3) il s'agit d'une série de Riemann (à noter que le est une constante car ne dépend pas de et il ne sert à rien si ce n'est à piéger l'élève). 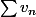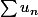Pour la 4), il s'agit d'une série à termes positifs, tu peux utiliser les théorèmes de comparaisons (du type si et que converge alors converge pourvu que les suites et sont de signe constant). Pour la 5) il faut discuter sur le paramètre : tu peux trouver un équivalent de selon si ou .