Bonjour,
Je poste ce message parce que je dois résoudre une équation de ce type:
Sinx+sin2x+sin3x=0(E).
[On calculera e^ix+e^2ix+e^3ix et sa partie imaginaire].
Mais je ne vois pas trop comment résoudre ça.
J'ai penser à faire un changement de variable ou à écrire ça en fonction de la formule d'Euler mais je ne pense pas que je pourrais résoudre ça avec cette formule.
Je peut écrire que sinx= (e^ix-e^-ix)/2i,et que Sinx+sin2x+sin3x= 0 <=>(e^ix-e^-ix)/2i+ (e^2ix-e^-2ix+-2e^0)/(2i)²+(e^3ix-e^3ix-3e^-ix+3e^ix)/(2i)^3.
Si quelqu'un pouvait m'éclairer.
Résoudre une équation avec des sinus x
7 messages
- Page 1 sur 1
Jjl a écrit:Bonjour,
Je poste ce message parce que je dois résoudre une équation de ce type:
Sinx+sin2x+sin3x=0(E).
[On calculera e^ix+e^2ix+e^3ix et sa partie imaginaire].
Mais je ne vois pas trop comment résoudre ça.
J'ai penser à faire un changement de variable ou à écrire ça en fonction de la formule d'Euler mais je ne pense pas que je pourrais résoudre ça avec cette formule.
Je peut écrire que sinx= (e^ix-e^-ix)/2i,et que Sinx+sin2x+sin3x= 0 (e^ix-e^-ix)/2i+ (e^2ix-e^-2ix+-2e^0)/(2i)²+(e^3ix-e^3ix-3e^-ix+3e^ix)/(2i)^3.
Si quelqu'un pouvait m'éclairer.
Pas besoin de faire appel aux complexes
Ou bien, on peut remarquer que :

équivaut à :
 + (e^{ix})^{2} + (e^{ix})^3 = 0)
et on pose ensuite : . On obtient ainsi une équation polynomiale simple à résoudre en
. On obtient ainsi une équation polynomiale simple à résoudre en  telle que :
telle que : ... etc.
... etc.
Je te laisse faire la suite tout seule, parce que, c'est un exercice sympas à faire, et il vaut mieux le faire seul pour que tu apprennes à acquérir des automatismes en maths qui te serviront à l'avenir. :happy3:.
Cordialement. :happy3:
équivaut à :
et on pose ensuite :
Je te laisse faire la suite tout seule, parce que, c'est un exercice sympas à faire, et il vaut mieux le faire seul pour que tu apprennes à acquérir des automatismes en maths qui te serviront à l'avenir. :happy3:.
Cordialement. :happy3:
Salut,
Vu les "indics" de l'énoncé, c'est assez clairement la méthode "barbu" qui est demandée dans l'exercice.
Par contre, l'équation à résoudre n'est pas^2+(e^{ix})^3=0) vu que, par exemple,
vu que, par exemple, ) n'est pas égal à
n'est pas égal à 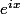 mais à la partie imaginaire de
mais à la partie imaginaire de 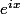 .
.
Donc je pense qu'il faut commencer par calculer la somme^2+(e^{ix})^3)
Le 1 disparaitra ensuite vu qu'on va prendre la partie imaginaire de S et il est là pour qu'on ait une gentille somme des 4 premiers termes d'une suite géométrique (attention à la formule donnant cette somme qui n'est pas valable tout le temps...)
Ensuite, on dira que l'équation de départ est équivalente à Im(S)=0 (à résoudre...)
EDIT : l'énoncé donne comme indic de calculer la somme S ci dessus sans le 1+... du début : en fait, ça ne change quasiment rein (mais je préfère avec le 1+...)
Vu les "indics" de l'énoncé, c'est assez clairement la méthode "barbu" qui est demandée dans l'exercice.
Par contre, l'équation à résoudre n'est pas
Donc je pense qu'il faut commencer par calculer la somme
Le 1 disparaitra ensuite vu qu'on va prendre la partie imaginaire de S et il est là pour qu'on ait une gentille somme des 4 premiers termes d'une suite géométrique (attention à la formule donnant cette somme qui n'est pas valable tout le temps...)
Ensuite, on dira que l'équation de départ est équivalente à Im(S)=0 (à résoudre...)
EDIT : l'énoncé donne comme indic de calculer la somme S ci dessus sans le 1+... du début : en fait, ça ne change quasiment rein (mais je préfère avec le 1+...)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
barbu23 a écrit:Ou bien, on peut remarquer que :
équivaut à : + (e^{ix})^{2} + (e^{ix})^3 = 0)
et on pose ensuite :. On obtient ainsi une équation polynomiale simple à résoudre en
telle que :
... etc.
Je te laisse faire la suite tout seule, parce que, c'est un exercice sympas à faire, et il vaut mieux le faire seul pour que tu apprennes à acquérir des automatismes en maths qui te serviront à l'avenir. :happy3:.
Cordialement. :happy3:
Oui comme je l'ai dit dans la méthode précédente,j'ai pensé tout comme toi à un changement de variable,mais c'est vraiment dommage que sinx n'est pas égal à e^ix,ça nous aurait bien simplifié la vie^^.
Mais c'est vrai qu'il faut travailler les automatisme,c'est très important
.Ben314 a écrit:Salut,
Vu les "indics" de l'énoncé, c'est assez clairement la méthode "barbu" qui est demandée dans l'exercice.
Par contre, l'équation à résoudre n'est pasvu que, par exemple,
n'est pas égal à
mais à la partie imaginaire de
.
Donc je pense qu'il faut commencer par calculer la somme^2+(e^{ix})^3)
Le 1 disparaitra ensuite vu qu'on va prendre la partie imaginaire de S et il est là pour qu'on ait une gentille somme des 4 premiers termes d'une suite géométrique (attention à la formule donnant cette somme qui n'est pas valable tout le temps...)
Ensuite, on dira que l'équation de départ est équivalente à Im(S)=0 (à résoudre...)
EDIT : l'énoncé donne comme indic de calculer la somme S ci dessus sans le 1+... du début : en fait, ça ne change quasiment rein (mais je préfère avec le 1+...)
Ah ok,j'ai compris ta méthode,mais ils aurait dû écrire "On calculera eîx+..." avant d'écrire résoudre vu que pour résoudre il faut faire cette addition...
Bref,je ferais ce calcule et je te tiendrais au courant.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
