Recherche de partie principale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 04 Jan 2008, 22:29
par Aspx » 04 Jan 2008, 22:29
Bonsoir !
J'ai un peu de mal sur une recherche de partie principale à cause d'une indétermination.
J'aimerais trouver un équivalent de

lorsque x tend vers 0.
Le problême vient du fait que n peut être infini... Si on avait eu

on aurait pu faire un DL puis conclure en étudiant le terme epsilonesque qui pose soucis.
Ici je vois pas vraiment comment lever l'indétermination...
Merci d'avance !

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 04 Jan 2008, 22:46
par fatal_error » 04 Jan 2008, 22:46
Bonsoir,
je pense que c'est bon.
Tu fixe le n. Qqsoit n aussi grand soit-il, tu as toujours un x tres petit tel que nx tende vers 0.
Ici, tu peux donc remplacer

avec X->0
et

D'où
^n X^n)
la vie est une fête

-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 04 Jan 2008, 23:07
par alben » 04 Jan 2008, 23:07
Bonsoir,
Ta fonction est monotone en n (positif). On peut encadrer la série par une intégrale ...
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 04 Jan 2008, 23:07
par Aspx » 04 Jan 2008, 23:07
Je comprend pas vraiment ce que tu fais. De plus
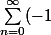^n n^{2n})
n'existe pas.
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 04 Jan 2008, 23:12
par Aspx » 04 Jan 2008, 23:12
Merci alben ! On trouve

dans ce cas j'ai l'impréssion.
Vraiment jte remercie, on nous apprend des méthodes de brutes parfois et c'est vrai que l'essentiel on a tendance à l'oublier !
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 04 Jan 2008, 23:15
par alben » 04 Jan 2008, 23:15
Oui, je trouve pareil :we:
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 04 Jan 2008, 23:37
par Aspx » 04 Jan 2008, 23:37
Maintenant, je cherche un équivalent en +infini de

(eh oui je ne vous avais pas tout dit :we: )
Aucun rapport avec ce qu'il précède, c'est juste dans le même exo.
Donc là encore même méthode, seulement comment s'y prendre pour le calcul de l'intégrale ?
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 04 Jan 2008, 23:48
par alben » 04 Jan 2008, 23:48
problème d'énoncé, il manque quelque chose !
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 04 Jan 2008, 23:53
par Aspx » 04 Jan 2008, 23:53
Non non il ne manque rien c'est une question en plus si tu veux, pour pas devoir refaire un thread.
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 04 Jan 2008, 23:56
par alben » 04 Jan 2008, 23:56
Ta formule ne veut rien dire n est à la fois la borne de la somme et la varaible à l'intérieur de cette somme.
Par ailleurs si c'est 1/ln(k), comme ln(1)=0, toutes les sommes parteilles sont infinies et l'équivalent c'est 1/0 !
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 04 Jan 2008, 23:58
par Aspx » 04 Jan 2008, 23:58
Excuse moi ! Je voulais dire

milles excuses.
-
alben
- Membre Irrationnel
- Messages: 1144
- Enregistré le: 18 Mai 2006, 21:33
-
 par alben » 05 Jan 2008, 00:12
par alben » 05 Jan 2008, 00:12
La primitive de 1/ln(t) ne s'exprime pas avec les fonctions usuelles, on a créé une fonction spéciale baptisée "logarithme intégral". On sait que vers l'infini elle se comporte comme x/ln(x) mais il te faut le retrouver par une autre méthode.
-
Aspx
- Membre Relatif
- Messages: 285
- Enregistré le: 25 Avr 2006, 13:12
-
 par Aspx » 05 Jan 2008, 00:33
par Aspx » 05 Jan 2008, 00:33
Cool :technicol une fonction spéciale !
Je vais me documenter merci !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 97 invités
