Racine de Polynomes complexe...
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
la-gueudine
- Membre Naturel
- Messages: 82
- Enregistré le: 20 Sep 2006, 13:08
-
 par la-gueudine » 11 Nov 2009, 20:55
par la-gueudine » 11 Nov 2009, 20:55
Bonsoir, je dois trouver les racines du polynomes suivant :
X^4 + 4iX^3 + (3+12i)X^2 - (24-14i)X+12 + 36i
pour le résoudre je doit démontrer que ce polynome à deux racines imaginaires pures. (l'exercice demande ensuite de factoriser par ces deux racines pour ensuite trouver les autres)
sauf que je ne sais pas comment faire pour montrer que ce polynome a deux racines imaginaires... quelqu'un peut-il me donner la piste pour démarrer s'il vous plait?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 11 Nov 2009, 20:58
par girdav » 11 Nov 2009, 20:58
Salut.
Trouve une condition sur

pour que

soit solution de l'équation.
-
la-gueudine
- Membre Naturel
- Messages: 82
- Enregistré le: 20 Sep 2006, 13:08
-
 par la-gueudine » 11 Nov 2009, 21:00
par la-gueudine » 11 Nov 2009, 21:00
Je remplace X par ai et je devrais trouver un a pour lequel c'est égal à zéro... sauf que ca marche pas
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 11 Nov 2009, 21:01
par girdav » 11 Nov 2009, 21:01
Ca devrait marcher?
Qu'est-ce qui ne va pas dans les calculs?
-
la-gueudine
- Membre Naturel
- Messages: 82
- Enregistré le: 20 Sep 2006, 13:08
-
 par la-gueudine » 11 Nov 2009, 21:03
par la-gueudine » 11 Nov 2009, 21:03
je trouve i(-11a+36) + 4a^3 - 17a+12 = 0
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 11 Nov 2009, 21:09
par wserdx » 11 Nov 2009, 21:09
Tu as à résoudre sur

une équation
P(X)=0
Ecris donc les deux équations pour
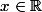
) = 0)
) = 0)
et montre que ces deux équations sur

ont des solutions communes
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 11 Nov 2009, 21:13
par girdav » 11 Nov 2009, 21:13
Je crois que tu t'es trompé(e). Je trouve:
 = 0)
et ça colle.
-
la-gueudine
- Membre Naturel
- Messages: 82
- Enregistré le: 20 Sep 2006, 13:08
-
 par la-gueudine » 11 Nov 2009, 21:16
par la-gueudine » 11 Nov 2009, 21:16
Re(P(x)) = X^4 + 3X^2 - 24X + 12
et Im(P(x)) = 4iX^3 +12iX^2+14X+36
c'est ca? maintenant il faut que je remplace X par ai dans chacune et que je trouve deux solutions qui marchent pour les deux?
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 11 Nov 2009, 21:22
par wserdx » 11 Nov 2009, 21:22
Euh non, tu ne m'as pas bien lu.
Tu remplaces

(complexe) par

avec

réel
et ensuite tu calcules la partie réelle et imaginaire.
Regarde le résultat donné par girdav...
-
la-gueudine
- Membre Naturel
- Messages: 82
- Enregistré le: 20 Sep 2006, 13:08
-
 par la-gueudine » 11 Nov 2009, 21:25
par la-gueudine » 11 Nov 2009, 21:25
j'arrive pas a trouver le meme résultat que toi girdav peut-on le reprendre ensemble par étape?
X^4 + 4iX^3 + (3+12i)X^2 - (24-14i)X+12 + 36i
en remplacant par ai
a^4 + 4a^3 - 3a^2 -12ia^2 - 24ai -14 +12 +36i
a^4 + 4a^3 - 3a^2 -12ia^2 - 24ai +2 +36i
-
la-gueudine
- Membre Naturel
- Messages: 82
- Enregistré le: 20 Sep 2006, 13:08
-
 par la-gueudine » 11 Nov 2009, 21:27
par la-gueudine » 11 Nov 2009, 21:27
j'arrive pas a trouver le meme résultat que toi girdav peut-on le reprendre ensemble par étape?
X^4 + 4iX^3 + (3+12i)X^2 - (24-14i)X+12 + 36i
en remplacant par ai
a^4 + 4a^3 - 3a^2 -12ia^2 - 24ai -14 +12 +36i
a^4 + 4a^3 - 3a^2 -12ia^2 - 24ai +2 +36i
a^4 + 4a^3 -3a^2 +2 +i(-12a^2-24a+36)
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 11 Nov 2009, 21:31
par wserdx » 11 Nov 2009, 21:31
il y a un "a" qui est passé à la trappe
tu as remplacé 14a par 14 il me semble...
-
la-gueudine
- Membre Naturel
- Messages: 82
- Enregistré le: 20 Sep 2006, 13:08
-
 par la-gueudine » 11 Nov 2009, 21:36
par la-gueudine » 11 Nov 2009, 21:36
X^4 + 4iX^3 + (3+12i)X^2 - (24-14i)X+12 + 36i
en remplacant par ai
a^4 + 4a^3 - 3a^2 -12ia^2 - 24ai -14a +12 +36i
en regroupant les imaginaires et les réels
a^4 + 4a^3 -3a^2+14a +12 +i(-12a^2-24a+36)
Im=0 pour a=-3 et a=1
comment je fais pour la partie réelle?
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 11 Nov 2009, 21:39
par wserdx » 11 Nov 2009, 21:39
Ben relis ce que j'ai écrit, vérifie que les racines que tu trouves pour la partie imaginaire sont aussi racines de la partie réelle!
-
la-gueudine
- Membre Naturel
- Messages: 82
- Enregistré le: 20 Sep 2006, 13:08
-
 par la-gueudine » 11 Nov 2009, 21:48
par la-gueudine » 11 Nov 2009, 21:48
Les solutions que j'ai trouvées ne vérifient pas Re =0 ...
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 11 Nov 2009, 21:52
par wserdx » 11 Nov 2009, 21:52
Et puis, il te reste aussi une erreur de signe,
c'est -14a et non pas 14a
-
la-gueudine
- Membre Naturel
- Messages: 82
- Enregistré le: 20 Sep 2006, 13:08
-
 par la-gueudine » 11 Nov 2009, 21:56
par la-gueudine » 11 Nov 2009, 21:56
c'est bon j'y suis arrivée. maintenant je factorise p(X) par (X+3i) et (X-i) pour obtenir p(X)=(X+3i)(X-i)(aX^2 + bX + c) je re-développe, j'identifie, ensuite je résous aX^2 + bX + c = 0 par une recherche classique de discriminant et ainsi de suite et j'aurai trouvé toutes mes racines de P(X) ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
