Rac(2) est il normal ?

par **mathelot** » 12 Jan 2007, 13:00

bonjour,

est un nombre algébrique irrationnel.
je me demandais si l'on pouvait en déduire des propriétés d'apparition de ses décimales de son équation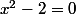

par un produit de séries tout simple. En particulier, comment démontrer si

est normal

par **yos** » 12 Jan 2007, 13:18

mathelot a écrit:si est normal

ça veut dire quoi? Je connais les extensions normales mais je ne vois pas le rapport.

par **tize** » 12 Jan 2007, 13:20

Il a une explication dans la wikipedia ici

par **yos** » 12 Jan 2007, 13:25

Merci Tize, c'est intéressant. Mais puisque la normalité de

est un pb ouvert, je saisis encore moins la question de Mathelot.

par **mathelot** » 12 Jan 2007, 21:11

Bonsoir Yos,
je me suis juste demandé ce que l'on pouvait déduire à propos des décimales de

si l'on injecte sa série:

dans l'équation:

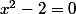
en élevant au carré la série selon le produit de convolution. ça doit donner des relations entre les décimales

qu'on aimerait exploiter à la manière probabiliste. (avec

)

par **mathelot** » 12 Jan 2007, 21:55

après quelques calculs, j'aboutis à la relation: