Quantificateurs

[eliascherif]

Bonjour,

J'ai un problème concernant les quantificateurs, je souhaite écrire la négation de "il existe un unique " mais je ne sais pas comment l'écrire un langage symbolique. Quelqu'un pourrait m'éclairer ?

merci

[Mimosa]

Bonjour

Il arrive qu'on note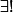 pour il existe unique, mais je ne crois pas que ce soit universel. Il reste la possibilité

[eliascherif]

merci de votre reponse mais je voulais savoir comment écrire la négation de ∃!
enfaite je dois écrire la négation de cette phrase en langage symbolique: la onction f s'annule exactement une fois sur I

[aviateur]

Il n'y a pas de symbole pour cette négation. de \exists! (par exemple) solution de l'équation E
Pour la négation tu diras simplement l'équation E n'a pas de solutions ou alors au,moins 2 solutions.

[eliascherif]

ok merci mais comment peut on écrire au moins 2 en langage symbolique ?(sachant que ∃= au moins 1)

[hdci]

Bonjour,
Il n'y a pas de notation pour "il existe au moins deux".
Mais on peut l'écrire ainsi :


Où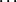 représente la propriété.

Ainsi, la négation de est