Ptit pb de détermination de réel

[dam77000]

Salut a tous :)

Alors voila j'ai un ptit pb de maths que j'arrive pas a résoudre si vous pouvez m'aider sa serait sympa :)

Donc avec f(x) = (-2x^2+7x-1)/(2x-1)

Jdois retouver a b et c de cette fonction la : f(x)=ax+b+c /(2x-1)

Merci d'avance :)

[mAroCaInEE]

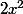
Désolée mais moi je n'arrive pas à comprendr tu as comment après tu as dans f(x) ax??
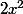
autre question est ce que (+7x-1)/2x+1?? ou seuelemnt 7x-1

[fatal_error]

Bonjour,

mise au même dénominateur, puis identification de a,b et c avec les puissance de x au numérateur

[dam77000]

Désolée mais moi je n'arrive pas à comprendr tu as 2x^2 comment après tu as dans f(x) ax??

Bonne question je comprend pas

[dam77000]

Alors jsuis arrivé a sa

a = -2x^2 / 2x-1

b= 7x / 2x-1

c= -1 facile celui la :p

Comment fais ton aprés pour dévelloper a et b ? Est ce sa ? ou je suis vraiment a la ramasse ? :p

[mAroCaInEE]

Par hasard tu n'as pas vu nos messages est ce que tu ne peux pas nous repondre??

[dam77000]

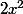
Désolée mais moi je n'arrive pas à comprendr tu as comment après tu as dans f(x) ax??
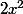
autre question est ce que (+7x-1)/2x+1?? ou seuelemnt 7x-1

Sisi j'ai vu dsl de ne pas l'avoir bien montré

C'est bien la totalité qui est divisé par 2x-1, j'ai remis les parenthese pour bien le montrer

[fatal_error]

on identifie avec les puissances :

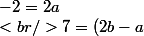etc

Et pour vérifier, tu teste avec une valeur quelqueconque de x, mettons 0, et tu regardes si tu as bien le même résultat avec la premiere ecriture de f et celle en fraction rationnelle

[mAroCaInEE]

on identifie avec les puissances :

Là c'est pas dam77000 qui va poser la question mais moi car là je ne comprend pas comment vous avez à trouver celà surtt passer de

[fatal_error]

...

[mAroCaInEE]

Ahhh je vois mnt mais bon là je dois poser la question à dam77000 est ce que c'est bien (ax+b)+c/2x+1 est ce que seulement c est sur (2x+1)??

[fatal_error]

Ahhh je vois mnt mais bon là je dois poser la question à dam77000 est ce que c'est bien (ax+b)+c/2x+1 est ce que seulement c est sur (2x+1)??

Et pour vérifier, tu teste avec une valeur quelqueconque de x, mettons 0, et tu regardes si tu as bien le même résultat avec la premiere ecriture de f et celle en fraction rationnelle

Soit tes coeffs sont faux, soit la fonction est mal écrite. Et comme tu as confiance, si c'est faux c'est que c'est la fonction :id:

Une autre méthode consiste a faire une division polynomiale (ca se trouve sur le web) :happy2: