Produit scalaire hermitien

[Ncdk]

Bonjour,

Je faisais un calcul sur les produits scalaires hermitiens, puis je suis arrivé au moment ou j'ai bloqué mais j'ai pas compris comment on passait d'une ligne à une autre.



J'ai voulu indicé d'une autre manière le second membre du produit scalaire pour éviter de faire des bêtises plus tard dans le calcul, mais gardons en tête que

Alors :

Maintenant on me dit que :

Je ne comprends pas cette égalité, si quelqu'un pourrait m'expliquer ça me servira pas mal que ce soit dans ou

[zygomatique]

salut

ben n'est-ce pas tout simplement la définition du produit scalaire hermitien ?

.....

[Ncdk]

En fait j'arrive juste pas à le démontrer à l'aide de la sesquilinéarité par exemple

[Ben314]

Tout comme zygomatique, je comprend pas bien où tu bloque...
Si c'est pourquoi le est devenu un quand on l'a "sorti" du produit hermitien, ça résulte effectivement de la définition : un produit hermitien n'est pas bilinéaire, il est linéaire par rapport à la première variable et "antilinéaire" (ou "semi-linéaire") par rapport à la deuxième variable.

[Ncdk]

Ah oui, non je vois, j'explique pas bien ce que je comprends pas.

Cette égalité, je me suis dit que j'allais développer un peu les sommes et voir comment on fait pour passer de l'autre côté, mais je maîtrise pas le produit scalaire et ce qu'on peut faire avec, pour moi en fait c'est pas immédiat, ça doit pas être sorcier, mais j'ai pas la raison du : pourquoi les sommes on peut les sortir et tout ça
Quand je développe les sommes, c'est pas naturel en fait, surement que je fais un mauvais calcul

[Ben314]

Essaye sur un exemple :
<a+b,c+d>
ça se "développe" comment ?
et <a+b+c+d , e+f> ?
Ne vois tu pas une "certaine analogie" avec un truc plus basique (qui est bilinéaire) ?
(attention à se méfier de cette "analogie" dans le cas hermitien où le truc n'est pas bilinéaire, mais "presque")

[Ncdk]

<a+b,c+d>=<a,c>+<a,d>+<b,c>+<b,d>

<a+b+c+d , e+f>=<a,e> + <a,f> + <b,e> + <b,f> + <c,e> + <c,f> + <d,e> + <d,f> ?

Pour l'analogie, non je vois pas, j'aurai peut-être dit les coordonnées d'un point, ou quelque chose dans ce style.

[Ben314]

Oui, c'est bien ça.
Pour moi, "l'analogie", c'est simplement celle avec le produit usuel sur R qu'on manipule depuis le primaire (et qui est évidement une forme bilinéaire).
Donc j'aurais tendance à dire de façon "simpliste" (donc attention...) qu'on "développe" n'importe quelle forme bilinéaire exactement de la même façon qu'on développe un produit de réels au collège.

Après, si tu arrive pas a voir que tout ces petits "cas particulier de développement", ça dit exactement la même chose que le cas général (avec deux symboles sigmas), je sais pas trop quoi te dire.
Tu peut évidement vérifier (par récurrence sur le nombre de termes) que la formule générale avec les deux sigma est correcte, mais perso, je le vois comme "complètement intuitif" le truc.

[Ncdk]

D'accord mais seulement quand nos formes bilinéaires sont à valeurs réelles ?

Après avec un produit scalaire hermitien, je peux pas développer de la même façon les deux petits exemples non ?

[Ben314]

(1) D'accord mais seulement quand nos formes bilinéaires sont à valeurs réelles ?
(2) Après avec un produit scalaire hermitien, je peux pas développer de la même façon les deux petits exemples non ?

(1) Non : ça serait à valeur dans autre chose, ça serait pareil (modulo que dans le "autre chose", il y ait bien une notion de produit et de somme et que tout soit commutatif bien sûr) : jusque là, c'est vraiment "de l'algèbre".
(2) Pour le moment, ça serait exactement la même chose avec un produit hermitien vu qu'il n'y a pas de différence en terme d'addition entre un produit scalaire (voire une forme bilinéaire quelconque) et un produit hermitien.
La différence n'apparait que lorsque tu veut "sortir" des multiplications (externes) par un scalaire :
Dans les deux cas
Ensuite, pour un produit scalaire, ça donne alors que, pour un produit hermitien, ça donne

[Ncdk]

Ah oui oui, l'algèbre en effet, j'étais resté sur l'exemple de base que tu m'as donné.

D'accord et ce conjugué de la forme hermitienne, quelle est la raison de son apparition, c'est une histoire de définition ou bien ça se démontre assez facilement avec une petite ligne ou deux ?

[Ben314]

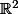
C'est extrêmement facile à comprendre : la norme usuelle sur c'est qui est un réel positif (et qui correspond à la racine carré de <X|X>).
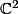
On voudrait faire un peu pareil dans , sauf que, si on pose bêtement alors
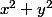
- Déjà ça veut pas dire grand chose vu que est un complexe et donc que sa racine carrée n'est pas bien définie.
- C'est plus que très fâcheux que le résultat ne soit pas réel positif : on aimerais que, comme dans le cas réel, ça corresponde à une notion de distance.
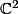
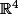
Si on est un peu plus malin, on se dit qu'au fond, c'est et que ça serait pas idiot de prendre comme définition (qui est bien un réel positif) c'est à dire en fait (avec des modules) soit encore .
Ca te conduit à définir l'équivalent du produit scalaire par et là, tu constate que ton truc n'est pas bilinéaire, mais "hermitien" à cause des conjugués que tu as été obligé de mettre sur les second termes.

Et il y a d'autres points de vu "naïfs" conduisant à la même conclusion : c'est ça la "bonne" définition.

[Ncdk]

D'accord merci
C'est clair maintenant