Problème résolution intégrale par changement de variables
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Guillaume1998
- Membre Naturel
- Messages: 42
- Enregistré le: 26 Fév 2019, 18:12
-
 par Guillaume1998 » 16 Nov 2019, 17:37
par Guillaume1998 » 16 Nov 2019, 17:37
Bonjour,
Je me pose une question pour la résolution de cette intégrale par changement de variables :
dx)
En effet, en posant u=cos(x), u'=-sin(x)=du/dx
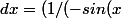))*du=(1/u')*du)
Cela donne :
}*\frac{1}{u'}=\frac{u'}{1+u}=ln(1+u)=ln(1+cos x))
Or ce résultat n'est pas le bon car en utilisant la méthode sin²x=1-cos²x on obtient pas le même résultat.
Voilà, si vous pouvez m'aider,
Merci
Modifié en dernier par
Guillaume1998 le 17 Nov 2019, 12:26, modifié 1 fois.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 16 Nov 2019, 18:32
par tournesol » 16 Nov 2019, 18:32
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 16 Nov 2019, 18:34
par tournesol » 16 Nov 2019, 18:34
-
mathelot
 par mathelot » 16 Nov 2019, 18:34
par mathelot » 16 Nov 2019, 18:34
Modifié en dernier par mathelot le 16 Nov 2019, 18:38, modifié 1 fois.

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 16 Nov 2019, 18:38
par anthony_unac » 16 Nov 2019, 18:38
Ah oui tout de suite, c'est beaucoup plus simple à intégrer ! (En plus ça fait appel à des identités remarquables de base)

-
Guillaume1998
- Membre Naturel
- Messages: 42
- Enregistré le: 26 Fév 2019, 18:12
-
 par Guillaume1998 » 16 Nov 2019, 20:43
par Guillaume1998 » 16 Nov 2019, 20:43
Merci pour la réponse mais justement comment retrouver le résultat là en utilisant la méthode de changement de variable. Je n’arrive pas à retrouver le résultat 1-pi/2 en posant u=cos(x)
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 16 Nov 2019, 20:45
par tournesol » 16 Nov 2019, 20:45
Il serait inrterressant et pédagogique de trouver l'erreur dans le raisonnement de Guillaume .
Je ne l'ai pas trouvé .

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 16 Nov 2019, 20:55
par anthony_unac » 16 Nov 2019, 20:55
Moi non plus car il a oublié de mettre les balises TEX. Je te propose Guillaume de récapituler pas à pas ton raisonnement en utilisant le bouton TEX
-
mathelot
 par mathelot » 16 Nov 2019, 21:33
par mathelot » 16 Nov 2019, 21:33
Ce qui est faux, c'est l'élément différentiel qu'il a
" oublié" d'ecrire: c'est u'(x) du et pas u'(x) dx
-
Yezu
- Membre Relatif
- Messages: 335
- Enregistré le: 14 Fév 2018, 12:29
-
 par Yezu » 16 Nov 2019, 21:46
par Yezu » 16 Nov 2019, 21:46
Guillaume1998 a écrit:Bonjour,
Je me pose une question pour la résolution de cette intégrale par changement de variables :
dx)
En effet, en posant
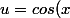, u'=-sin(x)=du/dx)
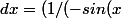))du=(1/u')du)
Cela donne :
}\frac{1}{u'}=\frac{u'}{1+u}=ln(1+u)=ln(1+cos x))
Or ce résultat n'est pas le bon car en utilisant la méthode sin²x=1-cos²x on obtient pas le même résultat.
Voilà, si vous pouvez m'aider,
Merci
Salut,
En posant
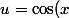)
,
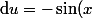 \mathrm{d} x)
. Ainsi, l'intégrant se réécrit :
}{1+\cos(x)}(-\sin(x)\mathrm{d}x) =<br />\dfrac{\sqrt{1-u^2}}{1+u}\mathrm{d}u)
(ton erreur est qu'en faisant le changement de variable, au numérateur tu n'as pas

mais plutôt

).
Ainsi :
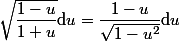
que tu peux facilement intégrer.
Edit : désolé; pas vu le msg de Mathelot.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 16 Nov 2019, 22:35
par Pisigma » 16 Nov 2019, 22:35
Bonsoir,
tout est dit, mais personnellement si on utilise le changement de variable de
Guillaume1998, je préfère procéder ainsi:
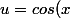, x=arcos(u))
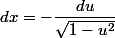
 dx}{1+cos(x)}=\int_1^0 \dfrac{(1-u^2)du}{\sqrt{1-u^2}(1+u)}=\int_1^0 \dfrac{(1-u)du}{\sqrt{1-u^2}}=...)
Rq: sans le changement de variable utilisé par
Guillaume1998 je procéderais comme
mathelot

-
anthony_unac
- Habitué(e)
- Messages: 1116
- Enregistré le: 29 Juin 2007, 23:31
-
 par anthony_unac » 16 Nov 2019, 22:46
par anthony_unac » 16 Nov 2019, 22:46
J'ai jamais pigé pourquoi on contraint un élève à résoudre un exercice avec une méthode et une seule. Rien de plus jouissif que de surmonter les difficultés d'un exercice avec des armes précieusement acquises au cours des années antérieures. Désolé je m'égare

-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 16 Nov 2019, 22:54
par tournesol » 16 Nov 2019, 22:54
Je n'ai toujours pas compris à quelle étape Guillaume s'est trompé .
-
Yezu
- Membre Relatif
- Messages: 335
- Enregistré le: 14 Fév 2018, 12:29
-
 par Yezu » 16 Nov 2019, 23:22
par Yezu » 16 Nov 2019, 23:22
Nous avons dis dans des messages précédents que son erreur a été de considérer
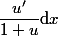
au lieu de
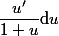
.
La première forme s'intègre immédiatement (
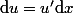
) mais pas la seconde.
-
Guillaume1998
- Membre Naturel
- Messages: 42
- Enregistré le: 26 Fév 2019, 18:12
-
 par Guillaume1998 » 17 Nov 2019, 12:32
par Guillaume1998 » 17 Nov 2019, 12:32
Yezu a écrit: Guillaume1998 a écrit:Bonjour,
Je me pose une question pour la résolution de cette intégrale par changement de variables :
dx)
En effet, en posant
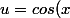, u'=-sin(x)=du/dx)
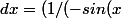))du=(1/u')du)
Cela donne :
}\frac{1}{u'}=\frac{u'}{1+u}=ln(1+u)=ln(1+cos x))
Or ce résultat n'est pas le bon car en utilisant la méthode sin²x=1-cos²x on obtient pas le même résultat.
Voilà, si vous pouvez m'aider,
Merci
Salut,
En posant
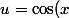)
,
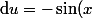 \mathrm{d} x)
. Ainsi, l'intégrant se réécrit :
}{1+\cos(x)}(-\sin(x)\mathrm{d}x) =<br />\dfrac{\sqrt{1-u^2}}{1+u}\mathrm{d}u)
(ton erreur est qu'en faisant le changement de variable, au numérateur tu n'as pas

mais plutôt

).
Ainsi :
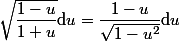
que tu peux facilement intégrer.
Edit : désolé; pas vu le msg de Mathelot.
-----------------------------
D'accord, merci pour la réponse mais pourquoi sin (x) devient

?
-
GaBuZoMeu
- Habitué(e)
- Messages: 6141
- Enregistré le: 05 Mai 2019, 09:07
-
 par GaBuZoMeu » 17 Nov 2019, 12:38
par GaBuZoMeu » 17 Nov 2019, 12:38
Peut-être parce que
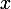
est dans

et que
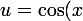)
?

-
Guillaume1998
- Membre Naturel
- Messages: 42
- Enregistré le: 26 Fév 2019, 18:12
-
 par Guillaume1998 » 17 Nov 2019, 13:00
par Guillaume1998 » 17 Nov 2019, 13:00
Ah oui ok c'est bon j'ai compris, c'est parce que sin²(x)=1-cos²(x) donc sin²(x)=1-u² et donc sin(x) =sqrt(1-u²)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
