Bonsoir à toutes et tous, j'éspère que tout le monde se porte bien. Voila, je suis actuellement en L1 éco gestion et pour mon premier TD de maths (à rendre dans une semaine environ) je bloque sur la première question.
Mon problème est le suivant:
Je ne me rapelle plus de la marche à suivre pour déterminer l'équation d'une fonction polynôme de degré 3, avec les seuls renseignements tels que:
-Une représentation graphique
-La courbe (C) passe par 3 points dont j'ai les coordonées.
-Deux tangentes sont facilement calculables.
-et enfin f(x)= ax^3+bx^2+cx+d
Voilà, merci d'avance pour tous les conseils de méthode qui arriveront, et je vous souhaite à toutes et tous une bonne nuit.
Problème de méthode
3 messages
- Page 1 sur 1
jusdemangue a écrit:Bonsoir à toutes et tous, j'éspère que tout le monde se porte bien. Voila, je suis actuellement en L1 éco gestion et pour mon premier TD de maths (à rendre dans une semaine environ) je bloque sur la première question.
Mon problème est le suivant:
Je ne me rapelle plus de la marche à suivre pour déterminer l'équation d'une fonction polynôme de degré 3, avec les seuls renseignements tels que:
-Une représentation graphique
-La courbe (C) passe par 3 points dont j'ai les coordonées.
-Deux tangentes sont facilement calculables.
-et enfin f(x)= ax^3+bx^2+cx+d
Voilà, merci d'avance pour tous les conseils de méthode qui arriveront, et je vous souhaite à toutes et tous une bonne nuit.
- avec les trois points tu as trois équations
- avec les tangentes tu as deux autres équations
5 équations, 4 inconnues. Merveilleux !
Salut,
si ca passe pas trois points :
 y_1=ax_1^3+bx_1^3+cx_1+d \\<br />(2) y_2=ax_2^3+bx_2^3+cx_2+d)
On peut faire (1)-(2) (ca élimine d) et (1-3) pour recup le troisieme point.
Avec l'aide des tangentes on trouve la dernière équation non liée (on veut déterminer a,b et c)
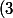 f'(q_1)=3aq_1^2+2bq_1+c\\<br />(3') f'(q_2)=3aq_2^2+2bq_2+c)
de même (3)-(3')
On obtient donc le système
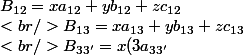+y(2b_{33' }))
Qu'on peut écrire sous forme matricielle :

si ca passe pas trois points :
On peut faire (1)-(2) (ca élimine d) et (1-3) pour recup le troisieme point.
Avec l'aide des tangentes on trouve la dernière équation non liée (on veut déterminer a,b et c)
de même (3)-(3')
On obtient donc le système
Qu'on peut écrire sous forme matricielle :
la vie est une fête 
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 38 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
