On sait qu'une opération des yeux à 90% de reussite.
On va realiser l'operation sur 5 patients.
soit X la variable aléatoire égale au nombre de reussite de l'opération sur 4 tentatives.
1. En supposant les resultats succés ou échec des 5 opérations soient indépendantes entre eux quel modele proposez vous pour X?
Je pensais à la loi binomiale
2/1.Quelle est la proba que l'opération rate 5fois ?
2/2.Quelle est la probabilité que l'opération reussisse au moins 3fois ?
3. Quelle est la probabilité que l'opération rate exactement 3fois ?
Pouvez vous me dire si mes calcules sont justes? merci
2/1. J'utilise la loi binomiale car y'a soit une reussite sois un echec.
1) Je comprend ce qu'on me demande
pour la 2/1) j'ai fais
ck xp^kxq^n-k
n
C5 x 0,9^5 x 0,1^0
5
2/2.
C3x 0,9^3 x 0,1^2
5
3/ m= n xp= 5x0,9 =4,5
P(X=>3) = 1 - P(x<3)
= 1-P(x=0)-¨P(x=1)-P(x=2)-P(x=1)
= 1- e^-4,5 x 4,5^0/0! - e^-4,5 x 4,5^1/1! - e^-4,5 x 4,5^2/2!-e^-4,5 x 4,5^3/3!
Probleme exercice de statistique sur loi binomiale, loi de poisson, loi normale
4 messages
- Page 1 sur 1
Bonjour baba11,
0. Je pense qu'il y a une petite erreur de frappe dans l'énoncé : X la variable aléatoire égale au nombre de réussites de l'opération sur 5 tentatives (une tentative par patient).
1. Tu as tout à fait raison de penser à une loi binomiale. Qu'est-ce qui te fait dire ça? Quel est l'évènement qui suit une loi de Bernoulli ici? Pourquoi est-ce que l'indépendance est importante? Et quels sont les paramètres de la loi binomiale à laquelle tu penses?
2/1.Quelle est la proba que l'opération rate 5fois ? ( je suppose que l'énoncé veut dire "cinq échecs consécutifs de l'opération, chaque tentative étant indépendante")
C'est difficile de comprendre ce que tu écris, sans parenthèses ni signe =.
Que signifient p et q dans ta formule?
Au final quel est le résultat de ton calcul? (il est juste, et le résultat se simplifie beaucoup)
Le plus important en fait, ce n'est pas vraiment le résultat du calcul mais la démarche et la justification : pour comprendre pourquoi c'est cette formule, cherche la probabilité que l'opération rate 1 fois, puis deux fois de suite, puis 3 fois de suite, etc. Normalement tu dois pouvoir en déduire la proba que l'opération rate fois de suite, avec
fois de suite, avec  un entier quelconque.
un entier quelconque.
2/2. Quelle est la probabilité que l'opération réussisse au moins 3fois
Attention à la subtilité de l'énoncé : on te demande opération réussie au moins trois fois, ça veut dire : trois fois ou quatre fois ou cinq fois. Tu as calculé la proba que l'opération réussisse exactement trois fois.
Pour cette probabilité, ton résultat est juste mais il ne veut rien dire tel quel, il faut que tu écrives une égalité entre la probabilité d'un certain évènement, et un nombre réel compris entre 0 et 1. Avec un signe =.
La formule que tu utilises est bien correcte, c'est celle de la loi binomiale. *
Pour répondre à l'énoncé il faut donc que tu rajoutes la proba de réussir 4 fois et la proba de réussir 5 fois.
3. Quelle est la probabilité que l'opération rate exactement 3fois ?
La déjà c'est mieux, ce que tu écris veut dire quelque chose : il y a bien une probabilité à gauche, un signe égal et un nombre entre 0 et 1 à droite.
Par contre ce n'est pas la bonne probabilité que tu calcules : l'évènement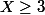 veut dire "opération réussie au moins trois fois". La question te demande de calculer p(X=2). En effet, trois échecs, c'est deux réussites, puisqu'il y a cinq opérations.
veut dire "opération réussie au moins trois fois". La question te demande de calculer p(X=2). En effet, trois échecs, c'est deux réussites, puisqu'il y a cinq opérations.
Ensuite, il y a une confusion avec la loi de Poisson : la ligne de calcul
est hors sujet ici : jusqu'à mention du contraire on le phénomène étudié suit toujours une loi binomiale, et non une loi de Poisson. La loi de Poisson est une approximation de la loi binomiale pour un très grand nombre, , de répétitions de l'épreuve (ici, l'opération des yeux). Mais c'est une approximation de mauvaise qualité ici puisque
, de répétitions de l'épreuve (ici, l'opération des yeux). Mais c'est une approximation de mauvaise qualité ici puisque  n'est pas très grand, il vaut 5. Il faut donc rester dans la loi binomiale.
n'est pas très grand, il vaut 5. Il faut donc rester dans la loi binomiale.
Ce que tu peux faire c'est calculer ton résultat sous forme d'un nombre entre 0 et 1, et le comparer avec celui donné par la loi binomiale. Tu pourras ainsi te rendre compte de l'erreur commise en utilisant la loi de Poisson au lieu de la loi binomiale quand les hypothèses d'approximation ne sont pas valables.
sous forme d'un nombre entre 0 et 1, et le comparer avec celui donné par la loi binomiale. Tu pourras ainsi te rendre compte de l'erreur commise en utilisant la loi de Poisson au lieu de la loi binomiale quand les hypothèses d'approximation ne sont pas valables.
Bon courage!
0. Je pense qu'il y a une petite erreur de frappe dans l'énoncé : X la variable aléatoire égale au nombre de réussites de l'opération sur 5 tentatives (une tentative par patient).
1. Tu as tout à fait raison de penser à une loi binomiale. Qu'est-ce qui te fait dire ça? Quel est l'évènement qui suit une loi de Bernoulli ici? Pourquoi est-ce que l'indépendance est importante? Et quels sont les paramètres de la loi binomiale à laquelle tu penses?
2/1.Quelle est la proba que l'opération rate 5fois ? ( je suppose que l'énoncé veut dire "cinq échecs consécutifs de l'opération, chaque tentative étant indépendante")
baba11 a écrit:pour la 2/1) j'ai fais
ck xp^kxq^n-k
n
C5 x 0,9^5 x 0,1^0
5
C'est difficile de comprendre ce que tu écris, sans parenthèses ni signe =.
Que signifient p et q dans ta formule?
Au final quel est le résultat de ton calcul? (il est juste, et le résultat se simplifie beaucoup)
Le plus important en fait, ce n'est pas vraiment le résultat du calcul mais la démarche et la justification : pour comprendre pourquoi c'est cette formule, cherche la probabilité que l'opération rate 1 fois, puis deux fois de suite, puis 3 fois de suite, etc. Normalement tu dois pouvoir en déduire la proba que l'opération rate
2/2. Quelle est la probabilité que l'opération réussisse au moins 3fois
baba11 a écrit:C3x 0,9^3 x 0,1^2
5
Attention à la subtilité de l'énoncé : on te demande opération réussie au moins trois fois, ça veut dire : trois fois ou quatre fois ou cinq fois. Tu as calculé la proba que l'opération réussisse exactement trois fois.
Pour cette probabilité, ton résultat est juste mais il ne veut rien dire tel quel, il faut que tu écrives une égalité entre la probabilité d'un certain évènement, et un nombre réel compris entre 0 et 1. Avec un signe =.
La formule que tu utilises est bien correcte, c'est celle de la loi binomiale. *
Pour répondre à l'énoncé il faut donc que tu rajoutes la proba de réussir 4 fois et la proba de réussir 5 fois.
3. Quelle est la probabilité que l'opération rate exactement 3fois ?
baba11 a écrit:3/ m= n xp= 5x0,9 =4,5
P(X=>3) = 1 - P(x<3)
= 1-P(x=0)-¨P(x=1)-P(x=2)-P(x=1)
= 1- e^-4,5 x 4,5^0/0! - e^-4,5 x 4,5^1/1! - e^-4,5 x 4,5^2/2!-e^-4,5 x 4,5^3/3!
La déjà c'est mieux, ce que tu écris veut dire quelque chose : il y a bien une probabilité à gauche, un signe égal et un nombre entre 0 et 1 à droite.
Par contre ce n'est pas la bonne probabilité que tu calcules : l'évènement
Ensuite, il y a une confusion avec la loi de Poisson : la ligne de calcul
baba11 a écrit:m= n xp= 5x0,9 =4,5
est hors sujet ici : jusqu'à mention du contraire on le phénomène étudié suit toujours une loi binomiale, et non une loi de Poisson. La loi de Poisson est une approximation de la loi binomiale pour un très grand nombre,
Ce que tu peux faire c'est calculer ton résultat
Bon courage!
Bonjour,
Je me joins à cette discussion parce que j'ai un problème similaire (je vais aussi publier un post sur ce même sujet).
J'ai un problème de statistiques où je dois calculer les probabilités selon les lois de poisson et binomiale avec des nombres fractionnels. Seul indice : trouver un multiple ou un dénominateur commun. Je ne comprends pas comment faire le calcul. J'ai essayé, mais je trouve des résultats aberrants. Auriez-vous des pistes pour m'aider à trouver la solution ?
Pour être précise : il y a une classe d'étudiants de 75%, avec 55% d'étudiants endettés. Je dois trouver la probabilité de trouver 4 étudiants endettés dans un échantillon de 10.
Un grand merci ! Je cherche depuis des heures et m'arrache les cheveux.
Je me joins à cette discussion parce que j'ai un problème similaire (je vais aussi publier un post sur ce même sujet).
J'ai un problème de statistiques où je dois calculer les probabilités selon les lois de poisson et binomiale avec des nombres fractionnels. Seul indice : trouver un multiple ou un dénominateur commun. Je ne comprends pas comment faire le calcul. J'ai essayé, mais je trouve des résultats aberrants. Auriez-vous des pistes pour m'aider à trouver la solution ?
Pour être précise : il y a une classe d'étudiants de 75%, avec 55% d'étudiants endettés. Je dois trouver la probabilité de trouver 4 étudiants endettés dans un échantillon de 10.
Un grand merci ! Je cherche depuis des heures et m'arrache les cheveux.
salut selon mes connaissances je pense qu'il y a une erreur au niveau de la question
2/1.Quelle est la proba que l'opération rate 5fois ?
en fait il veut dire qu'il y a 5 échec sur 5 opération et par la suite 0 succès(réussite) sur 5 opération
or X : la variable aléatoire décrivant le nombre de réussite alors il faut déterminer non pas P(X=5) mais plutot
p(X=0)= 5C0 * (0.9)^0 * (1-0.9)^5
et de meme pour la question 3 : exactement 3 échecs càd exactement 2 succès
p(X=2)=5C2 * (0.9)^2 *(1-0.9)^3 :lol3:
2/1.Quelle est la proba que l'opération rate 5fois ?
en fait il veut dire qu'il y a 5 échec sur 5 opération et par la suite 0 succès(réussite) sur 5 opération
or X : la variable aléatoire décrivant le nombre de réussite alors il faut déterminer non pas P(X=5) mais plutot
p(X=0)= 5C0 * (0.9)^0 * (1-0.9)^5
et de meme pour la question 3 : exactement 3 échecs càd exactement 2 succès
p(X=2)=5C2 * (0.9)^2 *(1-0.9)^3 :lol3:
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
