Probas/Integration
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
robby3
- Membre Naturel
- Messages: 54
- Enregistré le: 30 Sep 2005, 18:13
-
par robby3 » 23 Mar 2008, 18:01
Bonjour tout le monde,
voilà au milieu d'un exercice je bloque sur deux "en déduire"... Voici l'énoncé.
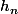
la densité de
j'ai vérifié que :
 = (\frac{n}{e})^n.\frac{\sqrt n}{n!}\exp(g_n(t))1_{]-\sqrt n ;+\infty[}(t) ou g_n(t) =-\sqrt n .t+n.\ln(1+t/\sqrt n ))
Ensuite j'ai montré que si
alors
\ge -t)
et que si
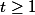
alors
\le -\frac 1 2)
Et là je ne parviens pas en déduire qu'il existe f intégrable tel que
)1_{]-\sqrt n ;+\infty[}(t) \le f(t))
.
Ensuite et bien en supposant cette condition vérifiée, je montre facilement que la limite de ce l'intégrale de
)1_{]-\sqrt n ;+\infty[}(t))
est en fait l'intégrale de Gauss (pour
) et vaut donc
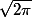
Il faut alors que j'en déduise la formule de Stirling
^n\sqrt{2\pi n})
En fait, je n'arrive pas à voir que
^n.\frac{\sqrt n }{n!} = \int_{\R} \exp(g_n(t))1_{]-\sqrt n ;+\infty[}(t))
Voilà, je vous remercie par avance de votre aide !
-
robby3
- Membre Naturel
- Messages: 54
- Enregistré le: 30 Sep 2005, 18:13
-
par robby3 » 23 Mar 2008, 21:06
quelqu'un a t-il une idée? :help: :cry:
par alavacommejetepousse » 23 Mar 2008, 23:21
je suis désolé
je ne peux comprendre un énoncé dans lequel il manque tant de données.
-
robby3
- Membre Naturel
- Messages: 54
- Enregistré le: 30 Sep 2005, 18:13
-
par robby3 » 24 Mar 2008, 11:54
Merci alavacommejetepousse
j'ai réussi!
Désolé,j'ai pas mi l'énoncé complet,il était vraiment trop long! :doh: :we:
Merci quand meme d'y avoir réfléchi! :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
