Probabilités / Convergence monotone.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 13 Oct 2012, 09:45
par Deluxor » 13 Oct 2012, 09:45
Bonjour à tous!
Je planche sur un exercice dont le but est de redémontrer des résultats de cours. Je vous indique ce que j'ai déjà fait ; merci de m'indiquer la voie à suivre pour résoudre les questions sur lesquelles je bloque, et de me corriger sur ce que j'ai fait.
---------------Enoncé---------------Soit
)
un espace de probabilité et
_{n\ge1})
une suite d'événements.
1. Le but de cette question est de redémontrer le résultat de cours suivant :
)
existe et
 \, = \, \mathbb{P}(\bigcup_{n\ge1} A_n))
(a) Montrer que
)
existe.
(b) On pose :
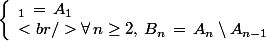
Montrer que :
 \, = \, \sum_{k=1}^n\mathbb{P}(B_k))
(c) Conclure.
2. Montrer à l'aide d'un contre-exemple que l'assertion
 \, = \, \mathbb{P}(\bigcup_{n\ge1} A_n))
n'est pas vraie en générale.
3. Montrer que cette assertion est cependant vraie dès que
=0)
, sans aucune autre hypothèse sur les événements

.
---------------Ce que j'ai fait---------------1. (a) //
(b) On a :
- les

deux à deux disjoints
-

-

Par

-additivité, on a :
 \, = \, \mathbb{P}(B_1 \, \cup \, B_2 \, \cup \, B_3 \, \cup \, ... \, \cup \, B_n))
 \, = \ \mathbb{P}(\bigcup_{k=1}^n B_k))
 \, = \ \sum_{k=1}^n\mathbb{P}(B_k))
(c) On a :
 \, = \ \sum_{k=1}^n\mathbb{P}(B_k))
Or :
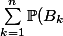 \, \nearrow \, \sum_{k=1}^{\infty} \mathbb{P}(B_k) \, = \, \mathbb{P}(\bigcup_{k=1}^{\infty} B_k) \, = \, \mathbb{P}(\bigcup_{n=1}^{\infty} A_n))
Donc :
) Soit :
Soit :  \, = \, \mathbb{P}(\bigcup_{n\ge1} A_n))
2. Considérons la mesure de comptage

sur

.
Soit :

Alors, on a :
 \, = \, 1)
MAIS :
 \, = \, \mu(\{ 0;1\}) \, = \, 2)
.
L'hypothèse de monotonie est donc fondamentale.
3. //
D'avance merci!
Deluxor
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 13 Oct 2012, 09:57
par cuati » 13 Oct 2012, 09:57
Bonjour,
quand tu as écrit //, c'est que c'est évident pour toi au c'est que tu ne sais pas ?
Sinon, pour la 2., je ne pense pas qu'il faille prendre une mesure de comptage puisque la question est posée avec
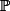
qui est normalement une proba. Prends une suite qui n'est pas croissante pour l'inclusion.
[EDIT] En fait il suffit d'adapter ce que tu as déjà écrit
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 13 Oct 2012, 10:17
par Deluxor » 13 Oct 2012, 10:17
cuati a écrit:Bonjour,
quand tu as écrit //, c'est que c'est évident pour toi au c'est que tu ne sais pas ?
Sinon, pour la 2., je ne pense pas qu'il faille prendre une mesure de comptage puisque la question est posée avec
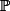
qui est normalement une proba. Prends une suite qui n'est pas croissante pour l'inclusion.
[EDIT] En fait il suffit d'adapter ce que tu as déjà écrit
Bonjour cuati,
Quand j'écris //, c'est que je ne sais pas résoudre les questions...
Pour la 2), étant donné qu'on nous donne un "espace de probabilité",
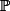
représente une mesure de probabilité, non? Donc, il n'est pas faux de prendre la mesure de comptage, qui est une mesure de probabilité, si?
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 13 Oct 2012, 10:34
par cuati » 13 Oct 2012, 10:34
Deluxor a écrit:Bonjour cuati,
Quand j'écris //, c'est que je ne sais pas résoudre les questions...
Pour la 2), étant donné qu'on nous donne un "espace de probabilité",
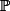
représente une mesure de probabilité, non? Donc, il n'est pas faux de prendre la mesure de comptage, qui est une mesure de probabilité, si?
La mesure de comptage n'est pas une mesure de proba !
Pour la 1.a.
)_n)
est une suite croissante de réels majorée (par 1 puisqu'il s'agit d'une proba) donc ...
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 13 Oct 2012, 10:54
par Deluxor » 13 Oct 2012, 10:54
cuati a écrit:La mesure de comptage n'est pas une mesure de proba !
Pour la 1.a.
)_n)
est une suite croissante de réels majorée (par 1 puisqu'il s'agit d'une proba) donc ...
Ahh!! Mais oui!! Merci beaucoup.
Est-ce bien rédigé?
1. (a)

, donc :
 \ge \mathbb{P}(A_{n+1}))
. Ainsi,
)_{n\ge1})
est une suite croissante.
De plus :  \le 1)
.
Donc, la suite
)_{n\ge1})
étant croissante et majorée, elle converge.
D'où l'existence de la limite.----
Pour la 2. : L'exemple de la mesure de comptage a été pris dans mon cours pour illustrer le fait que l'assertion n'était pas vraie si l'hypothèse de monotonie n'était pas vérifiée. Serait-ce donc une erreur? Dois-je prendre une suite particulière comme contre-exemple?
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 13 Oct 2012, 11:00
par cuati » 13 Oct 2012, 11:00
Attention au sens de l'inégalité, c'est
\leq\mathbb{P}(A_{n+1}))
----
Pour la 2. : L'exemple de la mesure de comptage a été pris dans mon cours pour illustrer le fait que l'assertion n'était pas vraie si l'hypothèse de monotonie n'était pas vérifiée. Serait-ce donc une erreur? Dois-je prendre une suite particulière comme contre-exemple?[/quote]
Pour la 2, elle montre bien que la monotonie est importante, mais il faut bien avoir à l'esprit que c'est une propriété vraie pour toutes les mesures. En ce qui concerne ton énoncé, on demande, il me semble, en plus de trouver un contre exemple dans le cas où la mesure est une proba.
Mais on peut prendre

si

est pair

si

est impair et
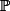
la proba uniforme sur [0,1]...
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 13 Oct 2012, 11:49
par Deluxor » 13 Oct 2012, 11:49
cuati a écrit:Attention au sens de l'inégalité, c'est
\leq\mathbb{P}(A_{n+1}))
Oups, erreur de LATEX...
Pour la 2. : L'exemple de la mesure de comptage a été pris dans mon cours pour illustrer le fait que l'assertion n'était pas vraie si l'hypothèse de monotonie n'était pas vérifiée. Serait-ce donc une erreur? Dois-je prendre une suite particulière comme contre-exemple?
Pour la 2, elle montre bien que la monotonie est importante, mais il faut bien avoir à l'esprit que c'est une propriété vraie pour toutes les mesures. En ce qui concerne ton énoncé, on demande, il me semble, en plus de trouver un contre exemple dans le cas où la mesure est une proba.
Mais on peut prendre

si

est pair

si

est impair et
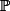
la proba uniforme sur [0,1]...[/quote]
Dans ce cas on a :
 \, = \, \frac{1}{2})
et
 \, = \, 1)
?
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 13 Oct 2012, 11:50
par cuati » 13 Oct 2012, 11:50
Deluxor a écrit:Oups, erreur de LATEX...
Pour la 2, elle montre bien que la monotonie est importante, mais il faut bien avoir à l'esprit que c'est une propriété vraie pour toutes les mesures. En ce qui concerne ton énoncé, on demande, il me semble, en plus de trouver un contre exemple dans le cas où la mesure est une proba.
Mais on peut prendre

si

est pair

si

est impair et
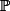
la proba uniforme sur [0,1]...
Dans ce cas on a :
 \, = \, \frac{1}{2})
et
 \, = \, 1)
?[/quote]
Oui, c'est bien cela
-
Deluxor
- Membre Rationnel
- Messages: 581
- Enregistré le: 29 Oct 2007, 12:00
-
 par Deluxor » 14 Oct 2012, 12:46
par Deluxor » 14 Oct 2012, 12:46
D'accord! Merci cuati! :)
Pour la 3), que faut-il faire?
-
cuati
- Membre Relatif
- Messages: 279
- Enregistré le: 27 Sep 2008, 16:40
-
 par cuati » 14 Oct 2012, 12:55
par cuati » 14 Oct 2012, 12:55
Deluxor a écrit:D'accord! Merci cuati!

Pour la 3), que faut-il faire?
=0)
signifie que

est un événement négligeable ! Or normalement tu sais qu'une union dénombrable d'ensembles négligeables est elle même négligeable (au pire tu le remontres).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
