Plongement !
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Déc 2009, 17:38
par barbu23 » 16 Déc 2009, 17:38
Bonjour : :happy3:
Est ce que :

definie par
 = \exp( 2i \pi t ) $)
est un plongement ? et pourquoi ?
Merci d'avance ! :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 16 Déc 2009, 17:41
par Nightmare » 16 Déc 2009, 17:41
D'après toi? Quelle est la définition d'un plongement?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Déc 2009, 17:42
par barbu23 » 16 Déc 2009, 17:42
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 16 Déc 2009, 17:43
par Nightmare » 16 Déc 2009, 17:43
Et donc? f est elle un plongement?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Déc 2009, 17:47
par barbu23 » 16 Déc 2009, 17:47
J'oublie comment on definit l'application linéaire :
 $)
et ce

! :hum:
Ben, il faut calculer le Jacobien, c'est ça ? :hein:
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Déc 2009, 17:50
par barbu23 » 16 Déc 2009, 17:50
}{\partial t} \frac{\partial \mathcal{Im}(f)}{\partial t}\end{pmatrix} $)
C'est ça ? :happy2:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 16 Déc 2009, 17:50
par Nightmare » 16 Déc 2009, 17:50
C'est la différentielle !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Déc 2009, 17:53
par barbu23 » 16 Déc 2009, 17:53
Oui mais consrètement, comment ? on calcule :
}{\partial t} \ \frac{\partial \mathcal{Im}(f)}{\partial t}\end{pmatrix} = \begin{pmatrix} - \sin (t) \ \cos (t) \end{pmatrix} $)
?
On fait quoi, après ? :happy2:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 16 Déc 2009, 17:57
par Nightmare » 16 Déc 2009, 17:57
En a une fonction d'une seule variable réelle, la différentielle au point x est l'application qui à h associe f'(x).h simplement.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Déc 2009, 18:08
par barbu23 » 16 Déc 2009, 18:08
c'est trucs là font partie du calcul differentiel ! j'ai oublié la moitié de ce cours là !
Ok,
 $)
est egale à quoi ? par contre

je suppose que c'est un vecteur ?
Merci d'avance ! :happy3:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 16 Déc 2009, 18:10
par Nightmare » 16 Déc 2009, 18:10
ben f'(x) c'est la dérivée de f, tu devrais savoir la calculer !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Déc 2009, 18:12
par barbu23 » 16 Déc 2009, 18:12
Oui, je pense que je l'ai calculé :
Oui mais consrètement, comment ? on calcule :
}{\partial t} \ \frac{\partial \mathcal{Im}(f)}{\partial t}\end{pmatrix} = \begin{pmatrix} - \sin (t) \ \cos (t) \end{pmatrix} $)
?
corrct ou non ? :hein:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 16 Déc 2009, 18:13
par Nightmare » 16 Déc 2009, 18:13
C'est une dérivée ça? Quel est ton niveau en mathématiques? Car tes énoncés sont d'un niveau bien supérieur à tes questions...
=2i\pi e^{2i\pi t})
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Déc 2009, 18:15
par barbu23 » 16 Déc 2009, 18:15
M1
C'est quoi donc l'expression de
 $)
:
(h) = 2i \pi \ \exp( 2 i \pi x ). h $)
et

est dans quel ensemble ?
MErci d'avance !
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Déc 2009, 19:42
par barbu23 » 16 Déc 2009, 19:42
Help please ! :happy3:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Déc 2009, 19:43
par Ben314 » 16 Déc 2009, 19:43
barbu23 a écrit:Bonjour : :happy3:
Est ce que :

definie par
 = \exp( 2i \pi t ) $)
est un plongement ? et pourquoi ?
Merci d'avance ! :happy3:
Tu prend quoi comme définition d'une variété pour que
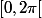
(fermé en 0) soit une variété ?
(c'est une variété "à bord")
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Déc 2009, 19:46
par barbu23 » 16 Déc 2009, 19:46

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Déc 2009, 19:50
par Ben314 » 16 Déc 2009, 19:50
A ce moment là (varièté sans bord), il faudrait que tu m'explique comment tu fabrique une carte au voisinage de 0....
Je cite :
"... que chacun de ses points admet un voisinage ouvert homéomorphe à
un ouvert de l'espace vectoriel topologique
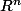
"
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 16 Déc 2009, 19:52
par barbu23 » 16 Déc 2009, 19:52
Ben314 a écrit:Tu prend quoi comme définition d'une variété pour que
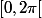
(fermé en 0) soit une variété ?
(c'est une variété "à bord")
c'est un espace topologique muni de la topologie induite !

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Déc 2009, 19:56
par Ben314 » 16 Déc 2009, 19:56
Je (re) pose ma question, comment produit tu une carte au voisinage de 0, c'est à dire un homéomorphisme de

sur un
ouvert de

?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités