PGCD((2^n)-1,(2^m)-1)

[naviss]

Bonjour a tous
J'ai un petit problème en arithmétique qui persiste depuis midi. Je dois montrer l'égalité suivante :


Pourriez vous m'aider ?

[Ben314]

Un premier truc pas difficile qui permet de faire "la moitié" du travail, et peu être de comprendre un peu comment ça marche, c'est de vérifier que le terme de droite divise celui de gauche, c'est à dire qu'il divise 2^n-1 ainsi que 2^m-1.
Sauf qu'en fait, ça n'apporte pas la preuve complète...

Pour cette dernière, essaye de faire comme pour l'algo d'euclide : si n>m et que l'on fait la division euclidienne de 2^n-1 par 2^m-1, ça va être quoi le quotient et, surtout, ça va être quoi le reste ?
Ensuite, il ne te reste plus qu'à écrire (comme l'algo d'euclide) que, si a=b*q+r alors
pgcd(a,b)=pgcd(b,r)...

[naviss]

Je ne vois pas trop comment montrer que le membre de droite divise les deux nombres de gauche. Je suis vraiment une quiche en arithmétique.

[Ben314]

Si alors, par définition, il divise (et ) donc.
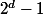
Le tout est de voir pourquoi divise forcément ...

[Doraki]

Pour faire un peu plus simple, 2^d-1 divise 2^nd-1 pour à peu près la même raison que 99 divise 999999.

[Finrod]

On peut "aussi" utiliser

Je met aussi entre guillemets car je n'ai pas compris la proposition de Doraki, donc c'est peut être la même chose.

[Ben314]

C'est effectivement la même chose : ce qu'a écrit Doraki, c'est ta formule dans laquelle on a pris X=100 et n=3 : 100^3-1 est divisible par 100-1.
(et le quotient est 1+100+100^2) niveau "sixième", ça s'écrirait
999999=99x10101 !!!
Effectivement, le résultat que je demandait est totalement concon... si on écrit les nombres en base 2...(et là, c'est pas forçément gagné pour tout le monde)

[naviss]

Ouinnn :cry:
Je suis vraiment nul je ne vois pas du tout ou tu veu en venir. je comprend pourquoi tu montre que dans A^B=C tu dit que C|A et C|B mais je ne comprend pas comment de ça je peu montrer mon égalité.