Voila, ne vous inquiétez pas je sais démontrer cette proposition , mon problème est qu'un amis ma dit que l'on pouvait la démontrer de la manière suivante :
On sait qu'il existe (u,v) appartenant a Z² tel que pgcd(a,b)=au+bv
donc (pgcd(a,b))² =(au+bv)²
(en développant on retomberait sur quelque chose de la forme )
=a²(...)+b²(...)
=pgcd(a²,b²)
avec le contenu des pointillé appartenant a Z . Nous avons arrêté notre discussion car le contenu des pointillé n'est pas entier mais la question que je me pose est : même si s'était le cas pourrait il vraiment conclure ?
(pgcd(a,b))²=pgcd(a²,b²)
9 messages
- Page 1 sur 1
Non, pas tout à fait, car ,s'il est vrai que :
"pgcd(a,b)=d" implique "il existe u et v entiers tels que au+bv=d"
la réciproque n'est pas vraie : par exemple, le fait que 12*2-9*2=6 n'implique pas que pgcd(12,9)=6 !!!!
Donc, à la fin du raisonnement, le fait que D=(..)a^2+(..)b^2 n'impliquerais pas que D=pgcd(a^2,b^2)
Remarque :
"il existe u et v tels que d=au+bv" est EQUIVALENT à "d est un multiple de pgcd(a,b)"
"pgcd(a,b)=d" implique "il existe u et v entiers tels que au+bv=d"
la réciproque n'est pas vraie : par exemple, le fait que 12*2-9*2=6 n'implique pas que pgcd(12,9)=6 !!!!
Donc, à la fin du raisonnement, le fait que D=(..)a^2+(..)b^2 n'impliquerais pas que D=pgcd(a^2,b^2)
Remarque :
"il existe u et v tels que d=au+bv" est EQUIVALENT à "d est un multiple de pgcd(a,b)"
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Bonjour,
Il me semble bien que l'on a équivalence pour tout d :
1) Si d=k.pgcd(a,b), comme il existe u' et v' tels que pgcd(a,b)=u'a+v'b, alors d=(ku')a+(kv')b est bien de la forme ua+vb.
2) Si d=ua+vb alors, comme le pgcd(a,b) divise à la fois a et b, il divise d et on a bien d=k.pgcd(a,b).
En fait, cette équivalence est souvent prise comme definition du pgcd : si a et b sont deux entiers alors, comme Z est principal, l'idéal aZ+bZ est engendré par un élément (unique si on demande qu'il soit positif) et c'est cet élément que l'on appelle le pgcd(a,b) (ou UN pgcd si on ne demande pas qu'il soit positif). Cette définition a le bon gout de pouvoir s'appliquer a tout anneau principal et pas seulement aux anneaux euclidiens.
Il me semble bien que l'on a équivalence pour tout d :
1) Si d=k.pgcd(a,b), comme il existe u' et v' tels que pgcd(a,b)=u'a+v'b, alors d=(ku')a+(kv')b est bien de la forme ua+vb.
2) Si d=ua+vb alors, comme le pgcd(a,b) divise à la fois a et b, il divise d et on a bien d=k.pgcd(a,b).
En fait, cette équivalence est souvent prise comme definition du pgcd : si a et b sont deux entiers alors, comme Z est principal, l'idéal aZ+bZ est engendré par un élément (unique si on demande qu'il soit positif) et c'est cet élément que l'on appelle le pgcd(a,b) (ou UN pgcd si on ne demande pas qu'il soit positif). Cette définition a le bon gout de pouvoir s'appliquer a tout anneau principal et pas seulement aux anneaux euclidiens.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re:
mais en développant il n'y a pas que a² et b² ! d'autre part,le théorème dont vous vous servez n'est qu'une implication!
Re: (pgcd(a,b))²=pgcd(a²,b²)
Bonsoir;
pour démontrer que \in \mathbb N^{*2} : (a) ^
^^2 = a^2) ^
^ , j'ai procédé comme suit :
, j'ai procédé comme suit :
Soit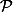 l'ensemble des nombres entiers naturels premiers.
l'ensemble des nombres entiers naturels premiers.
Pour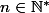 , la décomposition de n en produit de facteurs premiers est
, la décomposition de n en produit de facteurs premiers est }) avec
avec ) la valuation p-adique de n .
la valuation p-adique de n .
 \in \mathbb N^{*2}) , on a
, on a 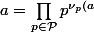}) et
et 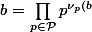}) ,
,
donc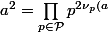}) et
et 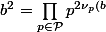}) ,
,
donc a ^ b =, \nu_p(b)\}}) ,
,
donc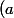 ^b
^b^2) =
= , \nu_p(b)\}}) ,
,
et ^
^ 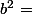
, 2\nu_p(b)\}}) =
= , \nu_p(b)\}})
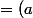 ^
^ ^2) .
.
Il y a d'autres démonstrations de cet exercice, mais j'aime toujours utiliser la décomposition en produit de facteurs premiers, quand l'occasion se présente.
pour démontrer que
Soit
Pour
donc
donc a ^ b =
donc
et
Il y a d'autres démonstrations de cet exercice, mais j'aime toujours utiliser la décomposition en produit de facteurs premiers, quand l'occasion se présente.
Re: (pgcd(a,b))²=pgcd(a²,b²)
On peut utiliser la bonne preuve de aymanemaysae pour n entier quelconque!
Re: Re:
touzani mohamed a écrit:mais en développant il n'y a pas que a² et b² ! d'autre part,le théorème dont vous vous servez n'est qu'une implication!
Bonjour !
Exact pour le carré mais en calculant
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 42 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
