Periodicité des reste de a^k par b...

par **gol_di_grosso** » 30 Sep 2007, 17:59

voila j'ai un problème :

Soient a,b deux entiers naturels non nuls et premiers entre eux.

1) Pour tout k appartenant à N, on note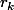

le reste de la division euclidienne de a^k par b.
Montrer que la suite

est periodique.

je pense dire que le nombre de possibilité de reste est fini.
ensuite prendre un reste

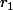
de

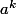
et montrer qu'à chaque fois que l'on a

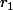
comme reste, on obtient un autre reste

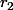
pour

,
mais je pense qui a un peu mieux non ???

par **fahr451** » 30 Sep 2007, 18:33

bonsoir

dans Z/bZ
classe (a) est inversible donc élément du groupe (Z/bZ)* et a donc un ordre fini

il existe T le plus petit entier strcitement positif tel que
classe(a)^T = classe(1)
la suite des restes est donc T périodique

par **gol_di_grosso** » 30 Sep 2007, 18:38

ouai je suis d'accord mais comment montrer que a est inversible dans Z/bZ, ou y a une définition que j'ai oublié...

par **abcd22** » 30 Sep 2007, 19:14

gol_di_grosso a écrit:ouai je suis d'accord mais comment montrer que a est inversible dans Z/bZ, ou y a une définition que j'ai oublié...

On a supposé a et b premiers entre eux.

par **gol_di_grosso** » 30 Sep 2007, 19:17

ouai mais je trouve plus la démo

par **fahr451** » 30 Sep 2007, 19:43

bezout

au +bv = 1

donne

classe(a)classe(u) = classe(1)

par **gol_di_grosso** » 30 Sep 2007, 20:06

oui en effet merci

par **yos** » 30 Sep 2007, 20:44

L'idée initiale de Gol di grosso est quand même bonne. D'autant plus que l'hypothèse "a et b premiers entre eux" est inutile (si on s'autorise la périodicité à partir d'un certain rang).

par **fahr451** » 30 Sep 2007, 22:06

oui mais là c'est périodicité stricte

Periodicité des reste de a^k par b...

periodicité des reste de a^k par b...

Qui est en ligne