Ogive équilatérale

[jeje56]

Bonjour,
Voici une ogive équilatérale : les arcs de cercle de centres A et B sont de rayon [AB].
Je ne parviens pas à exprimer le rayon r du petit cercle en fonction de R=AB/2...
Merci de votre aide.

[chan79]

Salut
Pythagore dans PIB, tout simplement
R=3r

[deltab]

Bonjour.

Bonjour,
Voici une ogive équilatérale : les arcs de cercle de centres A et B sont de rayon [AB].
Je ne parviens pas à exprimer le rayon r du petit cercle en fonction de R=AB/2...
Merci de votre aide.

Quelle est la nature du triangle AIP?
Peut-on exprimer AP et IP en fonction de r et R?

[siger]

Bonsoir

soit K le point de contact entre l'arc d'ogive AC et le cercle de centre P
K, Pet B sont alignes
les deux triangles PBI et KCP sont rectangles et semblables :
(sauf erreur!) KC/AB= KP/PI = CP/PB
d'ou KC en fonction de CP = CI-PI
puis dans les differents triangles rectangles PB, CP, ...
d'ou KP = r

[jeje56]

j'ai trouvé :
IP=r+R et
AP²=R²+(r+R)²
je ne sais pas comment continuer ...
merci de votre aide

[chan79]

j'ai trouvé :
IP=r+R et
AP²=R²+(r+R)²
je ne sais pas comment continuer ...
merci de votre aide

on a AP=2R-r

tracer (AP)

[MacManus]

Bonjour,

R² + (R+r)² n'est pas égal à (2R-r)²
AP ne vaut donc pas 2R-r

[edit]: bon, ben oui puique R=3r, je retire ce que j'ai dit ^^

[jeje56]

on a AP=2R-r

Comment le justifier ?... Il faut prouver l'alignement des points...

[Ben314]

Salut,
Deux cercles sont tangents extérieurement [respectivement intérieurement] si et seulement si la distance entre leurs centres respectifs est égale à la somme [respectivement différence] entre leurs rayons respectifs.
La preuve de ce résultat... va dépendre de la définition que tu donne à "cercles tangents". si tu prend comme définition le fait qu'ils ont un point commun où leurs tangentes respectives sont confondues alors c'est immédiat vu que la tangentes à un cercles en un point M du cercle est perpendiculaire aux rayon d'extrémité M : ça te donne immédiatement l'alignement des deux centres et du pont de tangence.

Là, il semble bien que ton dessin est fait de façon à ce que le cercle de centre P et de rayon r soit tangent à celui de centre A et de rayon 2R donc...

[jeje56]

Super, merci Ben pour la justification. Je retrouve bien R=3r.

[deltab]

Bonsoir

Bonjour,

R² + (R+r)² n'est pas égal à (2R-r)²
AP ne vaut donc pas 2R-r

[edit]: bon, ben oui puique R=3r, je retire ce que j'ai dit ^^

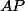
On cherche à exprimer en fonction de et vaut bien (Voir justification donnée par Ben314). On a donc l'équation en à résoudre: .

[MacManus]

Oui merci j'avais bien compris ces explications

[chan79]

salut
Je prolonge:
Et si le rayon du cercle rouge est 1, quel est celui des cercles verts ?
Ca peut se faire sans le théorème de Descartes

[Ben314]

A mon avis, la question, c'est plutôt "quel est celui des cercles bleus ?" (tu est daltonien ? :ptdr: )


ET... je trouve 6/11 comme rayon du cercle bleu si le rouge et de rayon 1.

[chan79]

c'est plutôt "quel est celui des cercles bleus ?"

.

Ah oui, tu as raison bien-sûr et c'est la bonne réponse :zen:

[Ben314]

Et le rayon du suivant ? et de celui d'après ? et du n-ième ?

(il y a une façon très simple de procéder n'utilisant pas non plus le théorème de Descartes)

[MacManus]

salut
Je prolonge:
Et si le rayon du cercle rouge est 1, quel est celui des cercles verts ?
Ca peut se faire sans le théorème de Descartes

Serait-il possible d'avoir une petite indication (si ce n'est pas donner la solution) car cet exercice m'intéresse, et j'ai fait des tonnes de traits, de triangles (parfois rectangles), de points, de projetés, de relations entre a, r et R et je trouve des trucs complètement tordus. Je n'y vois et n'y comprends plus rien... :smoke2:

ps: oui j'ai noté a le nouveau rayon (celui des cercles bleus donc). je trouve a=0.5

[chan79]

Serait-il possible d'avoir une petite indication (si ce n'est pas donner la solution) car cet exercice m'intéresse, et j'ai fait des tonnes de traits, de triangles (parfois rectangles), de points, de projetés, de relations entre a, r et R et je trouve des trucs complètement tordus. Je n'y vois et n'y comprends plus rien... :smoke2:

ps: oui j'ai noté a le nouveau rayon (celui des cercles bleus donc). je trouve a=0.5

Salut



Une méthode( en attendant celle de Ben314, peut-être ) :zen:
Al Kashi dans IPJ: (1+r)²=4²+(3+r)²-2*4(3+r)cos
Al Kashi dans AJI: (6-r)²=3²+(3+r)²+2*3(3+r)sin

car

on élimine avec cos² x+sin²x=1

[Ben314]

La méthode que j'ai employé, c'est d'utiliser les inversions : via une inversion centrée au point de tangence du cercle vert et du cercle noir (celui de droite par exemple) ces deux cercles deviennent des droites parallèles et les différents "petits cercles" (le rouge puis le bleu puis éventuellement les suivants) sont des cercles tangents aux deux droites (parallèles) et tangents entre eux : ils ont tous le même rayon et leurs centres sont régulièrement espacés sur une même droite.
Y'a plus qu'a utiliser le résultat qui donne le rayon R' de l'image C' d'un cercle C(O,R) par une inversion de rapport centré en : et ça donne où R est le rayon du cercle noir et n=0 correspond au plus grand cercle tangent au noir et au vert (centré en (-?,0)).
Sur ton dessin, le rouge correspond à n=2 et le bleu à n=3.

[MacManus]

Salut

Une méthode( en attendant celle de Ben314, peut-être ) :zen:
Al Kashi dans IPJ: (1+r)²=4²+(3+r)²-2*4(3+r)cos
Al Kashi dans AJI: (6-r)²=3²+(3+r)²+2*3(3+r)sin

car

on élimine avec cos² x+sin²x=1

D'accord, j'ai pensé à utiliser Al-Kashi mais que dans un seul triangle (en l'occurence le bleu) mais je ne savais pas quoi faire cette relation.
Merci pour ta réponse, je l'ai bien comprise, je vais regader celle proposée par Ben314 maintenant.