Bonjour,
Je cherche à démontrer que le trèfle
=\{(cos(t)+2cos(2t),sin(t)-2sin(2t),2sin(3t)),t\in[0;2\pi]\})
est
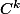
-difféomorphe à
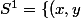\in R^2, x^2+y^2=1\})
.
Le but est donc de trouver un
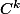
-difféomorphisme

de
)
dans
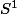
, ou inversement, "X est difféomorphe à Y" étant une relation d'équivalence.
Je partirais plutôt sur une application
)
dans
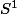
, qui à tout élément
)
, associerait un élément
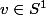
.
Soit donc
)
. Il existe donc
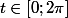
tel que
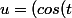+2cos(2t),sin(t)-2sin(2t),2sin(3t)))
Je cherche à montrer la bijectivité de l'application

.
Avant cela, comment définir

? ^^
On aurait
=x^2+y^2-1)
par exemple, et on pourrait choisir une combinaison astucieuse des trois coordonnées dépendantes de t pour obtenir
=0)
?
Bref, pouvez-vous m'aiguiller sur ce genre d'exercices ?
Merci d'avance pour vos indications.
