Morphismes de Frobénius

[busard_des_roseaux]

Bj,


Peux t on utiliser le morphisme de Frobénius

pour étudier la divisibilté d'un coefficient binomial ?

en écrivant l'exposant
en base q, le binôme donne



On voit que l'on fait le produit d'un certain nombre (fini) d'éléments
, en nombre inférieur ou égal à q, d'images résultats des composées
successives
où

Avec x,y et un corps de nombres bien choisis, est-ce que l'on n'arrive pas à qqe chose ? :doh:

[busard_des_roseaux]

up,up.... :we:

Quelqu'un peut regarder si on obtient une propriété de divisibilité par q
du coefficient binomial ?

sinon ,qq1 peut m'expliquer comment marche un morphisme de Frobénius
sur un corps fini ?

une fois donnée l'explication, j'essayerai de bien choisir les


(les sont les chiffres de l'exposant n en base q et x,y choisis comme on veut)

[Nightmare]

Salut :happy3:

Je voudrais bien t'aider mais je n'ai pas compris ce que tu voulais...Tu voudrais trouver un critère, en utilisant l'endomorphisme de Frobenius, de divisibilité de n'importe quel coef. binomial par un nombre quelconque q?

[busard_des_roseaux]

Salut :happy3:

Je voudrais bien t'aider mais je n'ai pas compris ce que tu voulais...Tu voudrais trouver un critère, en utilisant l'endomorphisme de Frobenius, de divisibilité de coef. binomial par un nombre quelconque q?

Bonjour NightMare ! :we:

En fait,oui. Pour q premier. Le souçi, c'est que je ne connais pas ce morphisme de Frobénius.
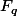
Il agit sur les corps finis ? Peux-t-on l'utiliser en liaison avec des séries formelles ? j'aimerai bien avoir une doc d'introduction ou un livre de référence. :doh:


merçi d'avance.