Minimums et maximums
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Marcet003
- Membre Naturel
- Messages: 88
- Enregistré le: 22 Avr 2022, 14:37
-
par Marcet003 » 08 Juin 2024, 21:32
Bonjour,
Soit la fonction suivante :
 = x^4 - 4x^3 + 3x^2 +2xy - y^2)
Pour trouver ses pts. stationnaires et leur nature, j'ai passé par un thm. avec la matrice hessienne et le signe de son determinant et de ses coefficients.
Mais j'ai aussi trouvé la forme quadratique suivante pour f :
 = -(y-x)^2 + x^2(x-2)^2)
et je me suis demandé si j'aurais pu déduire facilement la nature des points stationnaires de f à partir de son expression quadratique. Et de manière plus générale, à quoi servent les formes quadratiques ?
Merci d'avance,...
-
GaBuZoMeu
- Habitué(e)
- Messages: 6125
- Enregistré le: 05 Mai 2019, 09:07
-
par GaBuZoMeu » 09 Juin 2024, 15:18
Bonjour,
Ce n'est pas une forme quadratique : une forme quadratique est un polynôme homogène de degré 2, et ton polynôme est de degré 4.
-
Marcet003
- Membre Naturel
- Messages: 88
- Enregistré le: 22 Avr 2022, 14:37
-
par Marcet003 » 09 Juin 2024, 22:48
Ah oui. Bon je crois que je ne pouvais rien tirer de mon expression alors...
-
GaBuZoMeu
- Habitué(e)
- Messages: 6125
- Enregistré le: 05 Mai 2019, 09:07
-
par GaBuZoMeu » 10 Juin 2024, 07:57
Ta fonction est de la forme
où
)
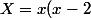et
.
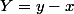
C'est la composée de
 \mapsto X^2-Y^2)
qui a comme point critique
)
(c'est un col), et de
\mapsto (x(x-2), y-x))
qui est un difféomorphisme local en dehors de
. Cela t'amène à considérer les points critiques de ta fonction de départ :
et
)
où ta fonction a des cols
et
)
où la fonction restreinte à la droite
a un maximum, et qu'il faut discuter.
Ça ne fait pas gagner grand chose par rapport à l'étude directe.
-
Marcet003
- Membre Naturel
- Messages: 88
- Enregistré le: 22 Avr 2022, 14:37
-
par Marcet003 » 10 Juin 2024, 16:03
D'accord merci !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
